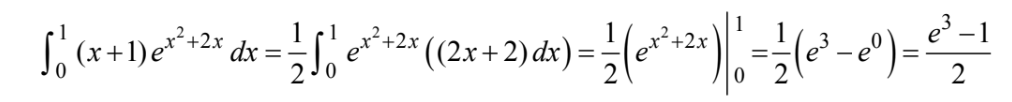Question
\(\int \frac{(x^{\frac{1}{3}}-4)^{5}}{6x^{\frac{2}{3}}}dx=\)
A \(\frac{(x^{\frac{1}{3}}-4)^{6}}{12}+C\)
B \(\frac{(x^{\frac{1}{3}}-4)^{6}}{6}+C\)
C \(\frac{5(x^{\frac{1}{3}}-4)^{4}}{2}+C\)
D \((3x^{\frac{1}{3}}-4)^{6}+C\)
Answer/Explanation
Question
\(\int_{0}^{8}\frac{dx}{\sqrt{1+x}}=\)
(A)1 (B)\( \frac{3}{2} \) (C)2 (D)4 (E)6
Answer/Explanation
Ans:D
Question
\(\int_{0}^{1}\frac{x^{2}}{x^{2}+1} dx\)=
(A)\(\frac{4-\pi }{4} \) (B)In 2 (C) 0 (D) \(\frac{1}{2}\) (E)\(\frac{4+\pi }{4}\)
Answer/Explanation
Ans:A
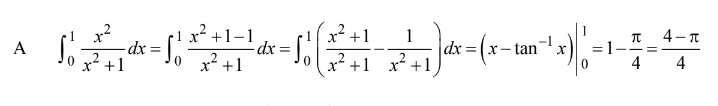
Question
\(\int_{0}^{3}(x+1)^{1/2}dx\)=
(A)\(\frac{21}{2}\) (B) 7 (C)\(\frac{16}{3}\) (D)\(\frac{14}{3}\) (E)\(-\frac{1}{4}\)
Answer/Explanation
Ans:D
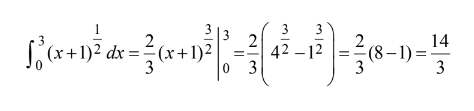
Question
\(\int x\sqrt{4-x^{2}}dx\)=
(A)\(\frac{\left ( 4-x^{2} \right )^{3/2}}{3}+C\) (B) \(-\left ( 4-x^{2} \right )^{3/2}+C\) (C)\(\frac{x^{2}\left ( 4-x^{2} \right )^{3/2}}{3}+C\) (D)\(-\frac{x^{2}\left ( 4-x^{2} \right )^{3/2}}{3}+C\) (E)\(-\frac{\left ( 4-x^{2} \right )^{3/2}}{3}+C\)
Answer/Explanation
Ans:E
Question
\(\int_{0}^{1}(x+1)e^{x^{2+2x}}dx\)=
(A)\(\frac{e^{3}}{2}\) (B)\(\frac{e^{3}-1}{2}\) (C)\(\frac{e^{4}-1}{2}\) (D)\(e^{3}-1 (E)e^{4}-e\)
Answer/Explanation
Ans:B