Question
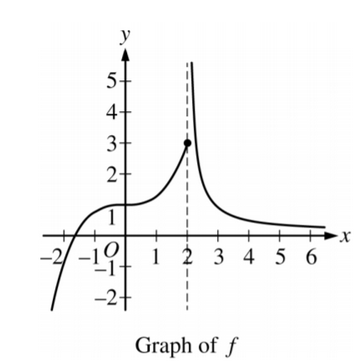
The graph of the function f is shown in the figure above. Which of the following statements must be false?
A \(lim_{x→2−}f(x)=3\)
B \(lim_{x→2+}f(x)=∞\)
C \(lim_{x→2}f(x)=f(2)\)
D \(lim_{x→∞}f(x)=0\)
Answer/Explanation
Question
The function h is defined by \(h(x)=\frac{x^{2}-9}{x-4}\). Which of the following statements must be true?
A \(\lim_{x\rightarrow 4^{-}}h(x)=-\infty \) and \(\lim_{x\rightarrow 4^{+}}h(x)=-\infty \)
B \(\lim_{x\rightarrow 4^{-}}h(x)=+\infty \) and \(\lim_{x\rightarrow 4^{+}}h(x)=-\infty \)
C \(\lim_{x\rightarrow 4^{-}}h(x)=-\infty \) and \(\lim_{x\rightarrow 4^{+}}h(x)=+\infty \)
D \(\lim_{x\rightarrow 4^{-}}h(x)=+\infty \) and \(\lim_{x\rightarrow 4^{+}}h(x)=+\infty \)
Answer/Explanation
Ans:C
Question
Let f be a function such that \(\lim_{x\rightarrow 3^{+}}f(x)=\infty\) . Which of the following statements must be true?
A \(\lim_{x\rightarrow 3^{-}}f(x)=\infty \)
B f is undefined at x=3.
C The graph of f has a vertical asymptote at x=3.
D The graph of f has a vertical asymptote at x=−3.
Answer/Explanation
Ans:C
Question
Let f be a function of x. If \(\lim_{x\rightarrow 2^{-}}f(x)=\infty\) and \(\lim_{x\rightarrow 2^{+}}f(x)=\infty\) , which of the following could be a graph of f ?
A 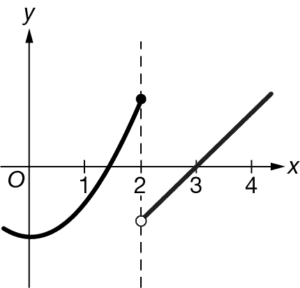
B 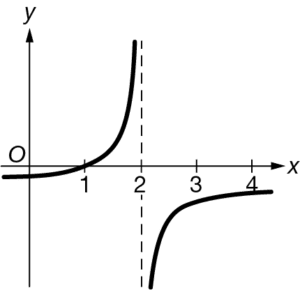
C 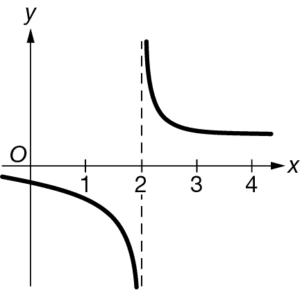
D 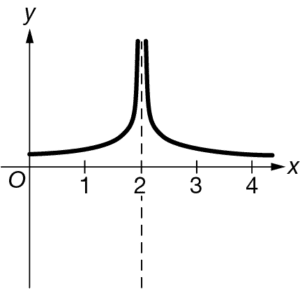
Answer/Explanation
Ans:D
