Question
If \(\frac{dy}{dx}=ysec^{2}x\)
(A)\(e^{tanx}+4 \) (B)\(e^{tanx}+5\) (C)\(5e^{tanx}\) (D)\(tanx+5\) (E)\(tanx+5e^{x}\)
Answer/Explanation
Ans:C
Question
If \(\frac{dy}{dx}=(1+lnx)\)y and if y = 1 when x = 1, then y =
(A)\(e^{\frac{x^2-1}{x^2}}\)
(B)\(1+lnx\)
(C)lnx
(D)\(e^{2x+xlnx-2}\)
(E)\(e^{xlnx}\)
Answer/Explanation
Ans:E
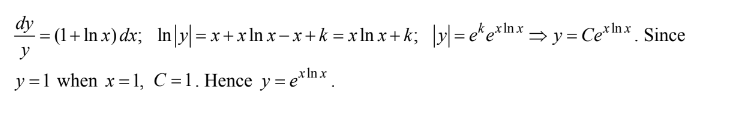
Question
If \(\frac{dy}{dt}=-2y \) and if y = 1 when t = 0, what is the value of t for which y =\( \frac{1}{2}\) ?
(A) \(-\frac{ln 2}{2}\) (B)\(-\frac{1}{4]\) (C) \(\frac{ln 2}{2}\) (D) \frac{\sqrt{2}}{2}\) (E) ln 2
Answer/Explanation
Ans:C
This is the differential equation for exponential growth.
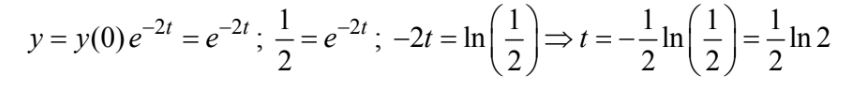
Question
If \( {dx}=sinxcos^{2}x \) and if y = 0 when \(x=\frac{\pi}{2}\), what is the value of y when x = 0 ?
(A) −1 (B) \(-\frac{1}{3}\) (C) 0 (D)\(\frac{1}{3}\) (E) 1
Answer/Explanation
Ans:B
