Question
If f ′ (x) and g'( x) exist and f'(x)>g'(x) for all real x, then the graph of y = f(x) and the graph of y= g(x )
(A) intersect exactly once.
(B) intersect no more than once.
(C) do not intersect.
(D) could intersect more than once.
(E) have a common tangent at each point of intersection.
Answer/Explanation
Ans:B
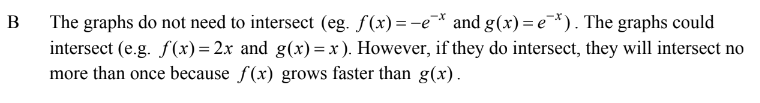
Question
If y is a function x such that 0 y′ > for all x and 0 y′′ < for all x, which of the following could be part of the graph of y = f(x )?
Answer/Explanation
Ans:B
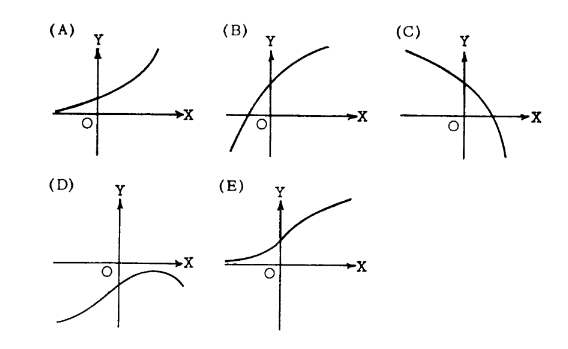
Question
Let f be a function that is continuous on the closed interval [−2,3] such that (0) f ′ does not exist, f ′(2) =0, and f ′′)x) < 0 for all x except x = 0. Which of the following could be the graph of f ?
Answer/Explanation
Ans:E
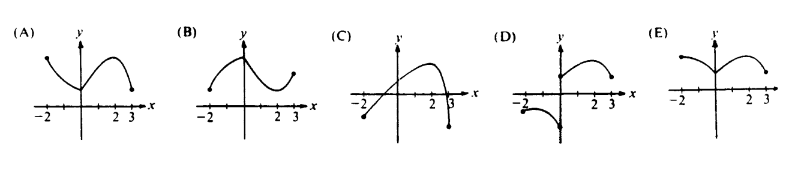
Question
Which of the following pairs of graphs could represent the graph of a function and the graph of its derivative?
(A) I only (B) II only (C) III only (D) I and III (E) II and III
Answer/Explanation
Ans:D
Question
If x+7y=29 is an equation of the line normal to the graph of f at the point ( 1, 4) , thenf ′ (1) =
(A) 7 (B) \(\frac{1}{7}\) (C) \(-\frac{1}{7}\) (D) \(-\frac{7}{29}\) (E) −7Ans:
Answer/Explanation
Ans:A
