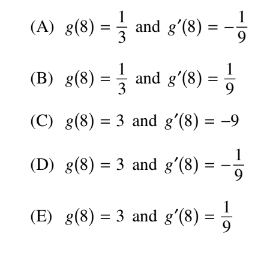Question
The point on the curve \(x^{2}+2y=0\) that is nearest the point\( \left ( 0,-\frac{1}{2} \right )\) occurs where y is
(A)\( \frac{1}{2}\)
(B)0
(C)\(-\frac{1}{2}\)
(D)-1
(E) none of the above
Answer/Explanation
Ans:B
Let L be the distance from 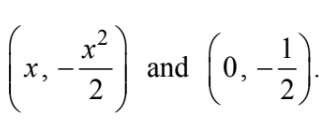
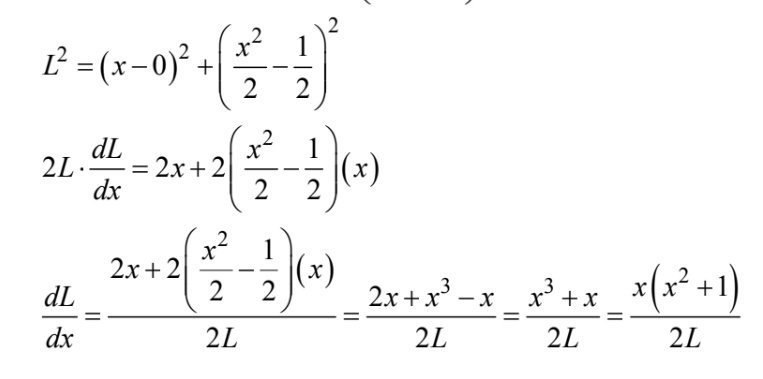
Question
The point on the curve \(x^{2}+2y=0\) that is nearest the point \( \left ( 0,-\frac{1}{2} \right )\) occurs where y is
(A) \( \frac{1}{2}\) (B) 0 (C)\( -\frac{1}{2}\) (D) −1 (E) none of the above
Answer/Explanation
Ans:B

Question

The table above gives values of the differentiable functions f and g and their derivatives at 1. x = 1 If h(x)= \((2f(x)+3)(1+g(x))\),then h'(1)
(A) -28 (B) -16 (C) 40 (D) 44 (E) 47
Answer/Explanation
Question
The functions f and g are differentiable. For all x,\( f(g(x)) =x\) and g(f(x))=x
If f(3)=8 and f'(3)=9,= what are the values of g(8)g'(8)