Question
At x = 0 , which of the following is true of the function f defined by \(f(x)=x^{2}+e^{(-2x)}\)?
(A) f is increasing.
(B) f is decreasing.
(C) f is discontinuous.
(D) f has a relative minimum.
(E) f has a relative maximum.
Answer/Explanation
Ans:B
Question
If \(f(x)=x+\frac{1}{x}\),then the set of values for which f increases is
(A) (−∞ , −1] ∪ [1 , ∞) (B) [−1,1] (C) (−∞ , ∞) (D) (0,∞ ) (E) (−∞ , 0)∪ (0 , ∞)
Answer/Explanation
Ans:A
Question
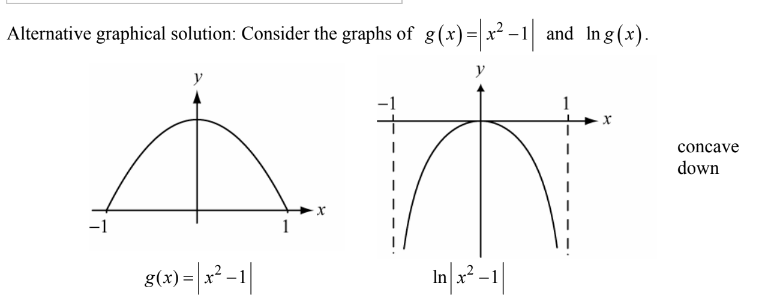
Which of the following is true about the graph of \(Y=In|x^{2}-1|\) in the interval ( −1,1 ) ?
(A) It is increasing.
(B) It attains a relative minimum at (0,0) .
(C) It has a range of all real numbers.
(D) It is concave down.
(E) It has an asymptote of x = 0 .
Answer/Explanation
Ans:D
For x in the interval \((-1,1),g(x)=|x^2-1=-(x^2-1) so y=lng(x)=ln(-x^2-1)\). Therefore
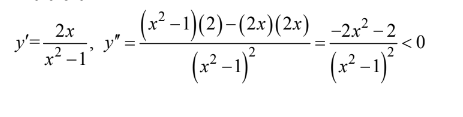
Question
If f(x)= , then the graph of f is decreasing for all x such that
(A)\(x<-2\) (B)\(-2<x<0\) (C)\(x>-2\) (D)x<0 (E)x>0
Answer/Explanation
Ans:B
