Question

During an evacuation drill, people leave a building at a rate of R( t) people per minute, where t is the number of minutes since the start of the drill. Selected values of R( t) are shown in the table above. Using a right Riemann sum with three subintervals and data from the table, what is the approximation of the number of people who leave the building during the first 15 minutes of the evacuation drill?
A 230
B 1150
C 1375
D 2075
Answer/Explanation
Question
Let R be the region in the first quadrant enclosed by the x-axis and the graph of \(y=ln(1+2x-x^{2}) \).If Simpson’s Rule with 2 subintervals is used to approximate the area of R, the approximation is
(A) 0.462 (B) 0.693 (C) 0.924 (D) 0.986 (E) 1.850
Answer/Explanation
Ans:C
Question
Let R be the region enclosed by the graph of \(y=1+ln(cos^4x)\) , the x-axis, and the lines \(x=-\frac{2}{3}\) and x=\(\frac{2}{3}\) . The closest integer approximation of the area of R is
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
Answer/Explanation
Ans:B
The area is given by
Question
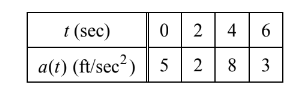
The data for the acceleration a ( t) of a car from 0 to 6 seconds are given in the table above. If the velocity at t = 0 is 11 feet per second, the approximate value of the velocity at t = 6 , computed using a left-hand Riemann sum with three subintervals of equal length, is
(A) 26 ft/sec (B) 30 ft/sec (C) 37 ft/sec (D) 39 ft/sec (E) 41 ft/sec
Answer/Explanation
Ans:E
