Question
If \(f(x)=\int _{0}^{x^{3}}\cos (t^{2})dt\) , then \(f'(\sqrt{\pi })=\)
A \(3π sin(\pi ^{3})\)
B \(cos(\pi ^{3})\)
C 3π cosπ
D 3π \(cos(\pi ^{3})\)
Answer/Explanation
Question
\(\int_{-1}^{2}\frac{|x|}{x}dx\) is
(A) –3 (B) 1 (C) 2 (D) 3 (E) nonexistent
Answer/Explanation
Ans:C
Question
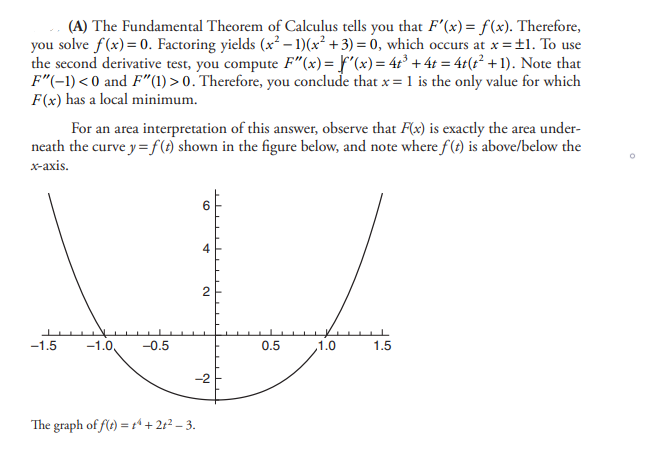
Let \(f(t)=t^{4}+2t^{2}-3\) and consider the function \(F(x)=\int_{-3}^{x}f(t)dt\) What are the x-value(s) for which F(x) has a local minimum?
(A) 1
(B) -1
(C) \(\pm \sqrt{3}\)
(D) ±1
Answer/Explanation
Ans:(A)
Question
If \(g(x)=\int_{0}^{x}\left ( \log _{2} (t-1)+\log _{2}(t+1)\right )dt\) find all x-values at which the line tangent to the graph of y = g(x) is horizontal.
(A) \(\sqrt{2}\)
(B) \(\sqrt{3}\)
(C) 2
(D) 3
Answer/Explanation
Ans:(A)
You are looking for solutions to g′(x) = 0, which by the Fundamental Theorem of Calculus is equivalent to solving f(x)=0. To begin, use properties of logarithms to simplify the equation:
\(\log _{2}(x-1)+\log _{2}(x+1)=0\Leftrightarrow \log _{2}\left [ (x-1)(x+1) \right ]=0\)
Exponentiating both sides of the last equation base 2, this becomes
\((x-1)(x+1)=1\Leftrightarrow x^{2}-2=0\)
