Question
if \(f(x)=(x^{2}+1)^{3}\) ,what is \(\lim_{x\rightarrow -1}\frac{f(x)-f(x+1)}{x+1}\) ?
A −24
B −8
C 0
D 12
Answer/Explanation
Question
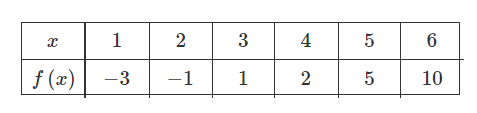
Selected values of a function f are shown in the table above. What is the average rate of change of f over the interval [1,6] ?
A \(\frac{6-1}{10-(-3)}\)
B \(\frac{10+(-3)}{6+1}\)
C \(\frac{10-(-3)}{6-1}\)
D \(\frac{(-3)+(-1)+1+2+5+10}{6}\)
Answer/Explanation
Ans:C
The average rate of change over the interval [1,6] is given by the difference quotient
Question
The graph of the function f, shown above, consists of three line segments. What is the average rate of change of f over the interval 1≤x≤7 ?
A −2
B 0
C \(\frac{1}{3}\)
D 3
Answer/Explanation
Ans:B
Question
The function f is given by f(x)=1+2sinx. What is the average rate of change of f over the interval \([0,\frac{\pi }{2}]\) ?
A \(\frac{4}{\pi }\)
B \(\frac{6}{\pi }\)
C \(\frac{8}{\pi }\)
D 2
Answer/Explanation
Ans:A
The difference quotient \(\frac{f(\frac{\pi }{2}-f(0))}{\frac{\pi }{2}-0}\) is the average rate of change of f over the interval \([0,\frac{\pi }{2}]\).
