Question
Let D represent the region bounded by the unit circle centered at the origin. Find the volume of the solid obtained by revolving D about the line x = 2.
(A)\(\frac{8\pi }{3}+4\pi ^{2}\)
(B) \(\frac{2\pi }{3}+\pi ^{2}\)
(C) \(\pi \left ( \frac{4}{3} +\sqrt{2}\right )\)
(D) \(\frac{8\pi }{3}\)
Answer/Explanation
Ans:(A)

Question
What is the volume of the solid generated by rotating about y = -1 the region in the first quadrant bounded by the curves y = 3 – x and \(y=\frac{x}{2}\) ?
(A) \(\frac{7\pi }{3}\)
(B) \(\pi \left [ \frac{7}{3} -\pi \ln 4\right ]\)
(C) \(\pi \left [ \frac{9}{2}+\ln 3 \right ]\)
(D) \(\pi \left [ \frac{10}{3}-4\ln 2 \right ]\)
Answer/Explanation
Ans:(D)

Question
The region enclosed by the graph of \(y=x^{2}\), the line x =2 and the x-axis is revolved about the y-axis. The volume of the solid generated is
(A) 8π (B) \(\frac{32}{5}\)π (C) \(\frac{16}{3}\)π (D) 4π (E) \(\frac{8}{3}\)
Answer/Explanation
Ans:A
Washers: ![]()
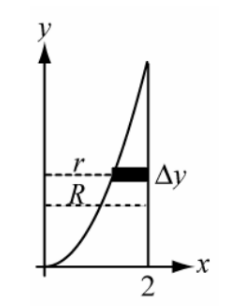
Volume ![]()
Question
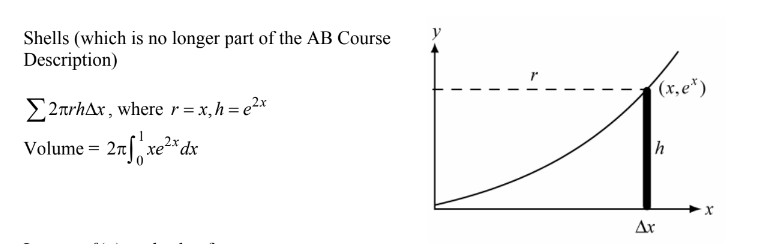
A region in the first quadrant is enclosed by the graphs of \(y=e^{2x}\),x = 1, and the coordinate axes.If the region is rotated about the y-axis, the volume of the solid that is generated is represented by which of the following integrals?
(A) \(2\pi\int_{0}^{1}xe^{2x}dx\)
(B)\(2\pi\int_{0}^{1}e^{2x}dx\)
(C)\(\pi\int_{0}^{1}e^{4x}dx\)
(D)\(\pi\int_{0}^{e}y ln ydy\)
(E)\(\frac{\pi }{4}\int_{0}^{e}ln^{2}ydy\)
Answer/Explanation
Ans:A