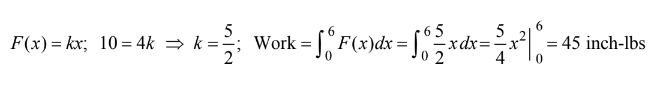Question
The position of an object attached to a spring is given by \(y(t)=\frac{1}{6}cos(5t)-\frac{1}{4}sin(5t) \), where t is time in seconds. In the first 4 seconds, how many times is the velocity of the object equal to 0?
(A) Zero
(B) Three
(C) Five
(D) Six
(E) Seven
Answer/Explanation
Ans:D
Question
Consider all right circular cylinders for which the sum of the height and circumference is 30 centimeters. What is the radius of the one with maximum volume?
(A) 3 cm (B) 10 cm (C) 20 cm (D) \(\frac{30}{\pi ^{2}}\) (E) \(\frac{10}{π}cm\)
Answer/Explanation
Ans:E
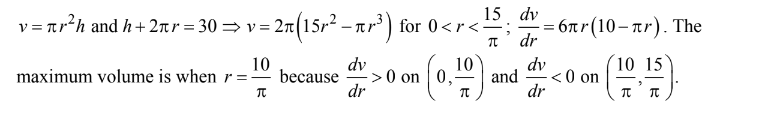
Question
A force of 10 pounds is required to stretch a spring 4 inches beyond its natural length. Assuming Hooke’s law applies, how much work is done in stretching the spring from its natural length to 6 inches beyond its natural length?
(A) 60.0 inch-pounds
(B) 45.0 inch-pounds
(C) 40.0 inch-pounds
(D) 15.0 inch-pounds
(E) 7.2 inch-pounds
Answer/Explanation
Ans:B