Question
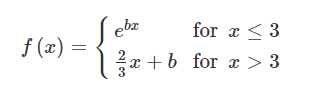
Let f be the function defined above. For what values of b is f continuous at x=3 ?
A 0.394 only
B 0.274 only
C −4.500 and 0.394
D −1.998 and 0.274
Answer/Explanation
Ans: D
Question
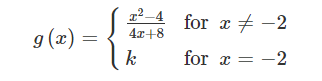
Let g be the function defined above, where k is a constant. For what value of k is g continuous at x=−2 ?
A −2
B −1
C −12
D 0
Answer/Explanation
Ans: B
In order for g to be continuous at x=−2, it is necessary that g(−2), which equals k, must equal \(\lim_{x\rightarrow 2}g(x)\)
\(\lim_{x\rightarrow -2}g(x)=\lim_{x\rightarrow -2}\frac{x^{2}-4}{4x+8}=\lim_{x\rightarrow -2}\frac{(x-2)(x+2)}{4(x+2)}=\lim_{x\rightarrow -2}\frac{(x-2)}{4}=-1\)
Question
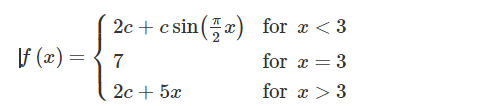
Let f be the function defined above. For what value of c, if any, is f continuous at x=3 ?
A −4
B 7
C −15
D There is no such c.
Answer/Explanation
Ans:D
Question
Which of the following are point(s) of discontinuity of the function \(f(x)=\frac{3x+1}{2x^{3}-8x^{2}-64x}\) ?
I. 0
II. 4
III. 8
(A) I only
(B) II only
(C) I and II only
(D) I and III only
Answer/Explanation
Ans:(D)
Rational functions are continuous everywhere except where the denominator is 0.
