Question
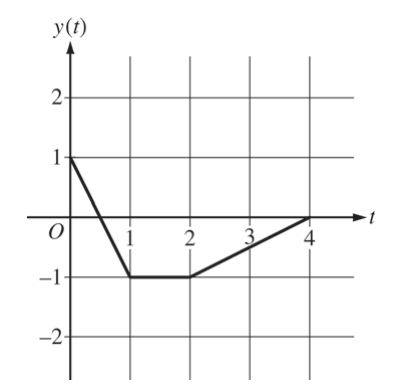
At time t, the position of a particle moving in the xy-plane is given by the parametric functions (x(t), y(t)), where \(\frac{dx}{dt}=t^{2}+sin(3t^{2}).\) The graph of y, consisting of three line segments, is shown in the figure above. At t = 0, the particle is at position (5, 1).
(a) Find the position of the particle at t = 3.
(b) Find the slope of the line tangent to the path of the particle at t = 3.
(c) Find the speed of the particle at t 3.
(d) Find the total distance traveled by the particle from t = 0 to t = 2.
Answer/Explanation
Ans:
(a) v(4) = 2.978716 > 0
v'(4) = -1.164000 < 0
The particle is slowing down since the velocity and acceleration have different signs.
(b) v(t) = 0 ⇒ t = 2.707468
v(t) changes from positive to negative at t = 2.707. Therefore, the particle changes direction at this time.
(c) \(x(0)=x(4)+\int_{4}^{0}v(t)dt\)
= 2 + (-5.815027) = -3.815
(d) \(Distance=\int_{0}^{3}v|(t)|dt=5.301\)
Question
For t ≥ 0, a particle is moving along a curve so that its position at time t is (x(t), y(t)). At time t = 2, the particle is at position (1, 5). It is known that \(\frac{dx}{dt}=\frac{\sqrt{t+2}}{e^{t}}and \frac{dy}{dt}=sin^{2}t.\)
(a) Is the horizontal movement of the particle to the left or to the right at time t = 2 ? Explain your answer.
Find the slope of the path of the particle at time t = 2.
(b) Find the x-coordinate of the particle’s position at time t = 4.
(c) Find the speed of the particle at time t = 4. Find the acceleration vector of the particle at time t = 4.
(d) Find the distance traveled by the particle from time t = 2 to t = 4.
Answer/Explanation
Ans:
(a) \(\frac{dx}{dt}|_{t=2}=\frac{2}{e^{2}}\)
Because \(\frac{dx}{dt}|_{t=2}=> 0\) the particle is moving to the right at time t = 2.
\(\frac{dx}{dt}|_{t=2}=\frac{dy/dt|_{t=2}}{dx/dt|_{t=2}}=3.055 (or 3.054)\)
(b) \(x(4)=1+\int_{2}^{4}\frac{\sqrt{t+2}}{e^{t}}dt=1.252 ( 1.252)\)
(c) Speed = \(\sqrt{(x'(4))^{2}+(y'(4))^{2}}=0.575 (or 0.574)\)
Acceleration = <x”(4), y”(4)>
= <-0.041, 0.989>
(d) Distance = \(=\int_{2}^{4}\sqrt{(x'(t))^{2}+(y'(t))^{2}}dt\)
= 0.651 ( or 0.650)
Question
| t (minutes) | 0 | 12 | 20 | 24 | 40 |
| v (t) (meters per minute) | 0 | 200 | 240 | -220 | 150 |
Johanna jogs along a straight path. For 0 ≤ t ≤ 40, Johanna’s velocity is given by a differentiable function v. Selected values of v(t), where t is measured in minutes and v(t) is measured in meters per minute, are given in the table above.
(a) Use the data in the table to estimate the value of v'(16).
(b) Using correct units, explain the meaning of the definite integral \(\int_{0}^{40}|v(t)|dt\) in the context of the problem.
Approximate the value of \(\int_{0}^{40}|v(t)|dt\) using a right Riemann sum with the four subintervals indicated in the table.
(c) Bob is riding his bicycle along the same path. For 0 ≤ t ≤ 10, Bob’s velocity is modeled by B(t) = t3 – 6t2 + 300, where t is measured in minutes and B (t) is measured in meters per minute.
Find Bob’s acceleration at time t = 5.
(d) Based on the model B from part (c), find Bob’s average velocity during the interval 0 ≤ t ≤ 10.
Answer/Explanation
Ans:
(a) \(v'(16)\approx \frac{240-200}{20-12}=5 meters/min^{2}\)
(b) \(\int_{0}^{40}|v(t)|dt\) is the total distance Johana jogs, in meters, over the time interval 0 ≤ t ≤ 40 minutes.
\(\int_{0}^{40}|v(t)|dt\approx 12\cdot |v(12)|+8\cdot |v(20)|+4\cdot |v(24)|+16\cdot |v(40)|\)
= 12 · 200+ 8 · 240 + 4 · 220 + 16 · 150
=2400 + 1920 + 880 + 2400
= 7600 meters
(c) Bob’s acceleration is B'(t) = 3t2 – 12t.
B'(5) = 3(25) – 12(5) = 15 meters/min2
(d) Avg vel \(\frac{1}{10}\int_{0}^{10}(t^{3}-6t^{2}+300)dt\)
\(\frac{1}{10}\left [ \frac{t^{4}}{4}-2t^{3}+300t \right ]_{0}^{10}\)
\(\frac{1}{10}\left [ \frac{10000}{4}-2000+3000 \right ]=350 meters/min\)
Question
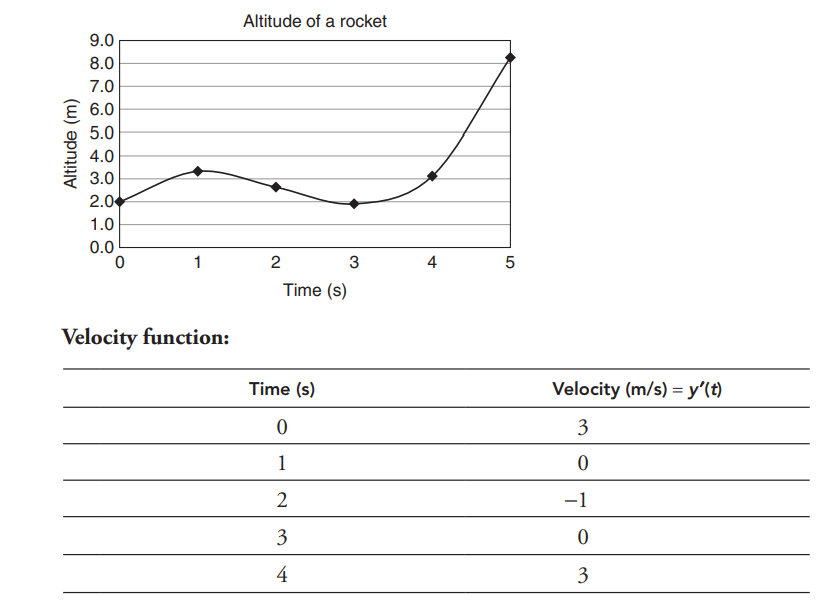
A student builds an experimental model rocket with a variable thrust engine. The test flight lasted for 5 s and the rocket’s altitude (in meters) could be described by the following function:
\(y(t)=\frac{1}{3}t^{3}-2t^{2}+3t+2\)
(A) What is the velocity function of the rocket (m/s)? What is the acceleration function of the rocket \((m/s^{2})\)?
(B) Make graphs of all three functions vs. time(s) for 0 to 5 s. Derive the maxima and minima for each graph (show your work).
Answer/Explanation
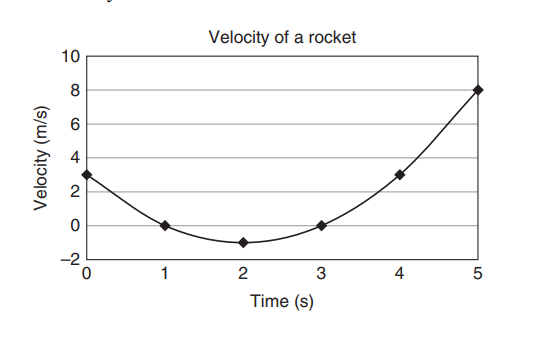
(A)Velocity is the first derivative of the altitude function: \(y'(t)=t^{2}-4t+3\)
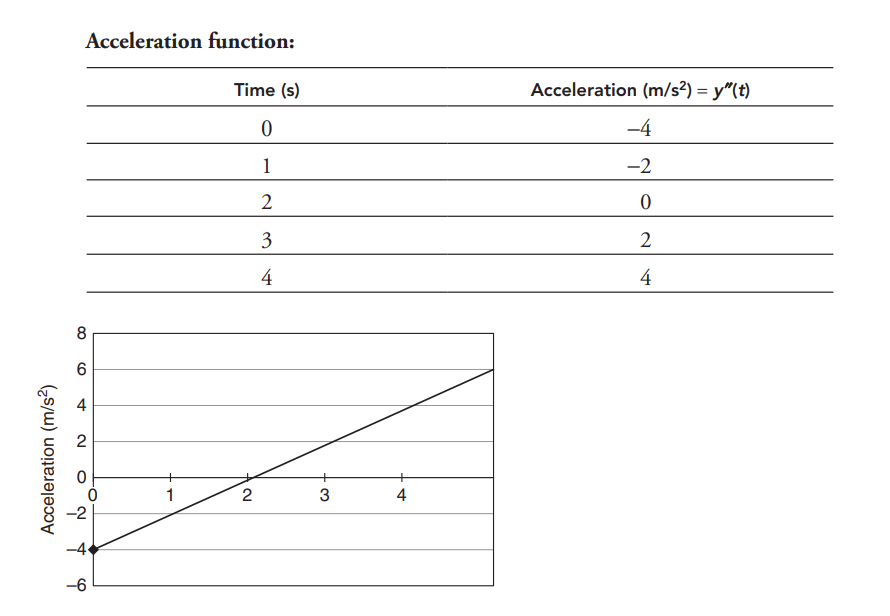
Acceleration is the second derivative of the altitude function: y”(t)=2t-4.
(B)
Crirtical Points:
\(y'(t)=x^{2}-4x+3\)
\(0=x^{2}-4x+3=(x-1)(x-3)\)
\(x-1=0\rightarrow x=1 y(1)=\frac{1}{3}(1)^{3}-2(1)+3(1)+2=3.3\) maximum (1,3.3)
\(x-3=0\rightarrow x=3 y(3)=\frac{1}{3}(3^{3})-2(3)^{2}+3(3)+2=2\) minimum (3,2)
Critical POints:
y”(t)=2x-4
0=2x-4
\(2x-4=0\rightarrow x=2 y'(2)=(2)^{2}-4(2)^{2}+3=-1\) minimum (2,-1)
\(y'(0)=(0)^{2}-4(0)^{2}+3=3\)
Question
A projectile is fired straight upward with a velocity of 256 ft/s. Its distance from the ground after being fired is given by \(s(t)=-16t^{2}+256t\), where t is the time in seconds since the projectile was fired.
(A) Write a velocity function for the projectile.
(B) What is the maximum altitude reached by the projectile?
(C) What is the acceleration at any time t?
(D) At what time does the projectile hit the ground?
Answer/Explanation
(A) v(t)=s(t)=−32t + 256
(B) At the maximum altitude, v(t)=0 so -32t+256=0 or t=8s. The projectile reaches its maximum altitude in 8 s. Find its position at 8s by applying \(s(8)=-16(8)^{2}+256(8)=-1024+2048=1024ft.\)
(C)\(a(t)=v’=-32ft/s^{2}\)
(D) When the projectile hits the ground, s(t) = 0. Therefore \(-16t^{2}+256t=0\).Factoring to solve for t, we find that t = 0, 16. The projectile lands in 16s.
Question
| t (minutes) | 0 | 2 | 5 | 8 | 12 |
| vA(t) (meters/minute) | 0 | 100 | 40 | 120 | 150 |
Train A runs back and forth on an east-west section of railroad track. Train A’s velocity, measured in meters per minute, is given by a differentiable function vA(t), where time t is measured in minutes. Selected values for vA(t) are given in the table above.
(a) Find the average acceleration of train A over the interval 2 ≤ t ≤ 8.
(b) Do the data in the table support the conclusion that train A’s velocity is -100 meters per minute at some time t with 5 < t < 8 ? Give a reason for your answer.
(c) At time t = 2, train A’s position is 300 meters east of the Origin Station, and the train is moving to the east.
Write an expression involving an integral that gives the position of train A, in meters from the Origin Station, at time t = 12. Use a trapezoidal sum with three subintervals indicated by the table to approximate the position of the train at time t = 12.
(d) A second train, train B, travels north from the Origin Station. At time t the velocity of train B is given by vB(t)= -5t2 + 60t + 25 , and at time t = 2 the train is 400 meters north of the station. Find the rate, in meters per minute, at which the distance between train A and train B is changing at time t = 2.
Answer/Explanation
Ans:
(a) Average accel = \(\frac{v_{A}(8)-v_{A}(2)}{8-2}=\frac{-120-100}{6}=-\frac{110}{3}m/min^{2}\)
(b) vA is differentiable ⇒ vA is continuous
vA (8) = -120 < – 100 < 40 = vA(5)
Therefore, by the Intermediate Value Theorem, there is a time t,
5 < t < 8, such that vA(t) = – 100.
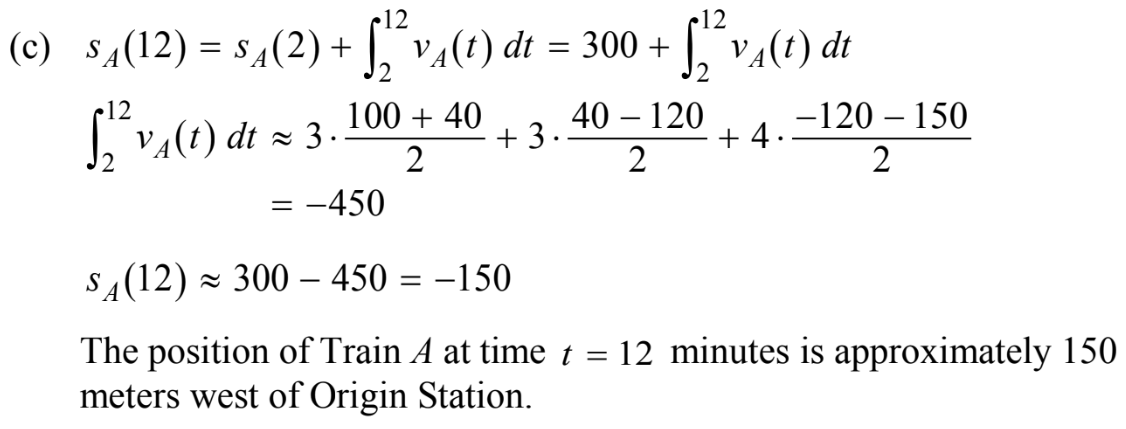
(d) Let x be train A’s position, y train B’s position, and z the distance between train A and train B.
\(z^{2}= x^{2}+y^{2}\Rightarrow 2z\frac{dz}{dt}=2x\frac{dx}{dt}+2y\frac{dy}{dt}\)
x = 300, y = 400 ⇒ z = 500
vB (2) = -20 + 120 + 25 = 125
\(500\frac{dz}{dt}=(300)(100)+(400)(125)\)
\(500\frac{dz}{dt}=(300)(100)+(400)(125)\) meters per minute
Question
A penny is dropped from rest off a building 150 ft tall. The position function of the penny is \(s(t)=-16t^{2}+150\), 2 where t ≥ 0 is in seconds. Find the following:
(A) the instantaneous velocity of the penny at t = 1 s
(B) the average velocity for the first 2 s
(C) the time when the penny will hit the ground.
Answer/Explanation
(A) v(t)=s'(t)=32t.v(1)=-32ft/s
(B) \(v_{average}=\frac{s(2)-s(0)}{2}=\frac{-16(2)^{2}+150-150}{2}=-32ft/s\)
(C)s(t)=0 when the penny hits the ground, so \(-16t^{2}+150=0\Rightarrow t\pm \sqrt{\frac{150}{16}}=\pm \frac{5\sqrt{6}}{4}\).Since you also know that \(t\geq 0,t=\frac{5\sqrt{6}}{4}=3.06s.\)
Question
At time t, a particle moving in the xy-plane is at position ( x(t), y(t)), where x(t) and y(t) are not explicitly given. For t ≥ 0, \(\frac{dx}{dt}=4t + 1 and \frac{dy}{dt}= sin(t^{2}).\) At time t = 0, x(0) = 0 and y(0) = -4.
(a) Find the speed of the particle at time t = 3, and find the acceleration vector of the particle at time t = 3.
(b) Find the slope of the line tangent to the path of the particle at time t = 3.
(c) Find the position of the particle at time t = 3.
(d) Find the total distance traveled by the particle over the time interval 0 ≤ t ≤ 3.
Answer/Explanation
Ans:
(a)
\(Speed =\sqrt{(\frac{dy}{dt})^{2}+(\frac{dx}{dt})^{2}}\)
\(\frac{dy}{dt}|_{t=3}=sin(3^{2})=sin9\)
\(\frac{dx}{dt}|_{t=3}=4(3)+1=13\)
\(Speed|_{t=3}=\sqrt{(sin9)^{2}+(13)^{2}}\)
Speed = 13.007
Acceleration Vector = \(\left \langle \frac{d^{2}x}{dt^{2}},{\frac{d^{2}y}{dt^{2}}} \right \rangle\)
\(\frac{dx}{dt}=4t +1; \frac{d^{2}x}{dt^{2}}=4\)
\(\frac{dy}{dt}=sin(t^{2}); \frac{d^{2}y}{dt^{2}}=2t cos (t^{2})\)
\(\frac{d^{2}x}{dt^{2}}|_{t=3}=4; \frac{d^{2}y}{dt^{2}}|_{t=3}=-5.467\)
Acceleration vector = <4, -5.467>
(b)
From part A,
\(\frac{dx}{dt}=\frac{\left ( \frac{dy}{dt} \right )}{\left ( \frac{dx}{dt} \right )}\) \(\frac{dy}{dt}|_{t=3}=sin9\)
\(\frac{dx}{dt}|_{t=3}=13\)
\(\frac{dy}{dx}= \frac{sin9}{13}=0.0317\)
(c)
x position at t = 3 is equal to x(0) + \(\int_{0}^{3}\frac{dx}{dt}dt\)
y position at t = 3 is equal to y(0) + \(\int_{0}^{3}\frac{dy}{dt}dt\)
\(x(3)=0+\int_{0}^{3}(4t+1)dt=21\)
\(y(3)=-4+\int_{0}^{3}sin(t^{2})dt=-3.226\)
At t = 3, the particle’s position is (21, -3.226)
(d)
Distance Travelled = \(\int_{0}^{3}\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right )^{2}}dt\)
\(=\int_{0}^{3}\sqrt{(4t+1)^{2}+sin^{2}(t^{2})}dt\)
Distance Travelled = 21.091
Question
| t (minutes) | 0 | 2 | 5 | 9 | 10 |
| H(t) (degrees Celsius) | 66 | 60 | 52 | 44 | 43 |
As a pot of tea cools, the temperature of the tea is modeled by a differentiable function H for 0 ≤ t ≤ 10, where time t is measured in minutes and temperature H(t) is measured in degrees Celsius. Values of H(t) at selected values of time t are shown in the table above.
(a) Use the data in the table to approximate the rate at which the temperature of the tea is changing at time t = 3.5. Show the computations that lead to your answer.
(b) Using correct units, explain the meaning of \(\frac{1}{10}\int_{0}^{10}H(t)dt\) in the context of this problem. Use a trapezoidal sum with the four subintervals indicated by the table to estimate \(\frac{1}{10}\int_{0}^{10}H(t)dt.\)
(c) Evaluate \(\int_{0}^{10}H'(t)dt.\) Using correct units, explain the meaning of the expression in the context of this problem.
(d) At time t = 0, biscuits with temperature 100 0C were removed from an oven. The temperature of the biscuits at time t is modeled by a differentiable function B for which it is known that
B'(t) = – 13.84e-0.173t . Using the given models, at time t = 10, how much cooler are the biscuits than the tea?
Answer/Explanation
Ans:
(a)
\(\frac{H(5)-H(2)}{5-2}=\frac{-8}{3}\frac{0_{C}}{min}\)
(b)
\(\frac{1}{10}\int_{0}^{10}H(t)dt\approx \frac{\left [2(\frac{66+180}{2}) +3(\frac{52+60}{2})+4(\frac{44+52}{2})+1(\frac{43+44}{2}) \right ]}{10}=52.95\)
This represents the average temperature in degree Celsius of the tea over the interval 0 ≤ t ≤ 10
(c)
\(\int_{0}^{10}H'(t)dt= H(10)-H(0)=43-66=-23^{0}C\)
This expression shows the total change in temperature in degree Celsius from t = 0 to t = 10.
(d)
\(B'(t)=-13.84e^{-.173t}\)
\(B(10)=\int_{0}^{10}-13.84e^{-.173t}+100 = 100-65.817 = 34.1827\)
43-341827 = 8.817
= 88170C Celsius
