Question
The region bounded by the x-axis and the part of the graph of y =cos x between \( x=-\frac{\pi }{2}\)and\( x=\frac{\pi }{2}\) is separated into two regions by the line x = k . If the area of the region for\( -\frac{\pi }{2}\leq x\leq k\) is three times the area of the region for\( k\leq x\leq \frac{\pi }{2}\), then k=
(A) arcsin\( \left ( \frac{1}{4} \right ) \) (B) arcsin\( \left ( \frac{1}{3} \right )\) (C) \(\frac{\pi }{6}\) (D)\(\frac{\pi }{4} (E) \frac{\pi }{3}\)
Answer/Explanation
Ans:C
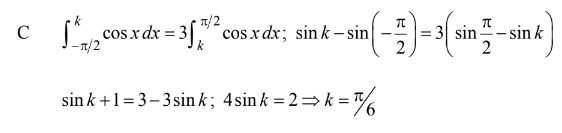
Question
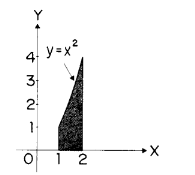
Calculate the approximate area of the shaded region in the figure by the trapezoidal rule, using divisions at \(x =\frac{4}{3}\) and \( x = \frac{5}{3}\).
(A) \(\frac{50}{27}\) (B) \(\frac{251}{108}\) (C)\(\frac{ 7}{3}\) (D) \(\frac{127}{54} \) (E) \(\frac{77}{27}\)
Answer/Explanation
Ans:D
Question
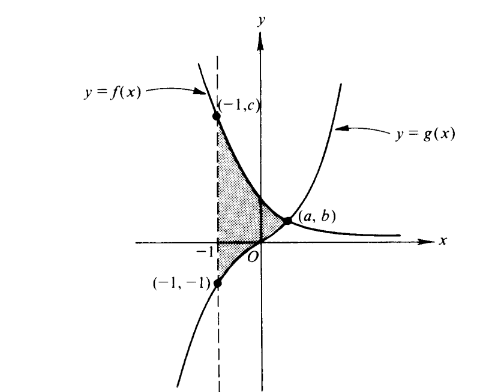
The curves \(y=f(x )\) and \(y=g( x) \) shown in the figure above intersect at the point \(( a , b)\) . The area of the shaded region enclosed by these curves and the line \(x = −1\) is given by
(A) \(\int_{0}^{a}(f(x)-g(x))dx+\int_{-1}^{0}(f(x)+g(x))dx\)
(B) \(\int_{-1}^{b}g(x)dx+\int_{d}^{c}f(x)dx\)
(C) \(\int_{-1}^{c}(f(x)-g(x))dx\)
(D) \(\int_{-1}^{a}(f(x)-g(x))dx\)
(E) \(\int_{-1}^{a}(|f(x)|-|g(x)|)dx\)
Answer/Explanation
Ans:D
Question
The area of the region enclosed by the graphs of \(y =x^2\) and \(y = x\) is
(A) \(\frac{1}{6}\) (B)\(\frac{1}{3}\) (C) \(\frac{1}{2}\) (D) \(\frac{5}{6}\) (E) 1
Answer/Explanation
Ans:A
