Question
The coefficient of \(x ^{3}\)in the Taylor series for\( e^{3x}\) about x = 0 is
(A) \(\frac{1}{6}\) (B) \(\frac{1}{3}\) (C)\frac{1}{2}\) (D) \(\frac{3}{2}\) (E) \(\frac{9}{2}\)
Answer/Explanation
Question
\(sin ( 2x) =\)
(A) $x-\frac{x^3}{3 !}+\frac{x^5}{5 !}-\ldots+\frac{(-1)^{n-1} x^{2 n-1}}{(2 n-1) !}+\ldots$
(B) $2 x-\frac{(2 x)^3}{3 !}+\frac{(2 x)^5}{5 !}-\ldots+\frac{(-1)^{n-1}(2 x)^{2 n-1}}{(2 n-1) !}+\ldots$
(C) $-\frac{(2 x)^2}{2 !}+\frac{(2 x)^4}{4 !}-\ldots+\frac{(-1)^n(2 x)^{2 n}}{(2 n) !}+\ldots$
(D) $\frac{x^2}{2 !}+\frac{x^4}{4 !}+\frac{x^6}{6 !}+\ldots+\frac{x^{2 n}}{(2 n) !}+\ldots$
(E) $2 x+\frac{(2 x)^3}{3 !}+\frac{(2 x)^5}{5 !}+\ldots+\frac{(2 x)^{2 n-1}}{(2 n-1) !}+\ldots$
Answer/Explanation
Ans:B
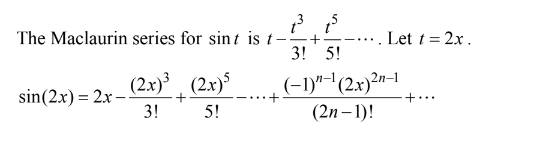
Question
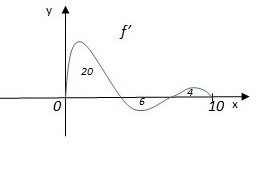
The graph of , \(f{}’\) the derivative of the function f, is shown above for \( 0\leq x\leq 10\). The areas of the regions between the graph of f ‘ and the x-axis are 20, 6, and 4, respectively. If f (0 ) = 2, what is the maximum value of f on the closed interval\( 0\leq x\leq 10\).?
(A) 16 (B) 20 (C) 22 (D) 30 (E) 32
Answer/Explanation
Question
A series expansion of \(\frac{sint}{t}\) is
(A)\(1-\frac{t^{2}}{3!}+\frac{t^{4}}{5!}-\frac{t^{6}}{7!}+…\)
(B)\(\frac{1}{t}-\frac{t}{2!}+\frac{t^{3}}{4!}-\frac{t^{5}}{6!}+…\)
(C)\(1+\frac{t^{2}}{3!}+\frac{t^{4}}{5!}+\frac{t^{6}}{7!}+….\)
(D)\(\frac{1}{t}+\frac{t}{2!}+\frac{t^{3}}{4!}+\frac{t^{5}}{6!}+…\)
(E)\(t-\frac{t^{3}}{3!}+\frac{t^{5}}{5!}-\frac{t^{7}}{7!}+…\)
Answer/Explanation
Ans:A
