Question
| t (years) | 2 | 3 | 5 | 7 | 10 |
| H(t) (meters) | 1.5 | 2 | 6 | 11 | 15 |
The height of a tree at time t is given by a twice-differentiable function H, where H (t) is measured in meters and t is measured in years. Selected values of H (t) are given in the table above.
(a) Use the data in the table to estimate H'(6 ). Using correct units, interpret the meaning of H'(6 ) in the context of the problem.
(b) Explain why there must be at least one time t, for 2 < t< 10 , such that H'(t) = 2.
(c) Use a trapezoidal sum with the four subintervals indicated by the data in the table to approximate the average height of the tree over the time interval 2 ≤ t ≤ 10.
(d) The height of the tree, in meters, can also be modeled by the function G, given by \(G(x)=\frac{100x}{1+x},\) where x is the diameter of the base of the tree, in meters. When the tree is 50 meters tall, the diameter of the base of the tree is increasing at a rate of 0.03 meter per year. According to this model, what is the rate of change of the height of the tree with respect to time, in meters per year, at the time when the tree is 50 meters tall?
▶️Answer/Explanation
Ans:
(a) \(H'(6)\approx \frac{H(7)-H(5)}{7-5}=\frac{11-6}{2}=\frac{5}{2}\)
H′(6) is the rate at which the height of the tree is changing, in meters per year, at time t = 6 years.
(b) \(\frac{H(5)-H(3)}{5-3}=\frac{6-2}{2}=2\)
Because H is differentiable on 3 ≤ t ≤ 5, H is continuous on 3 ≤ t ≤ 5.By the Mean Value Theorem, there exists a value c, 3 < c < 5, such that H ‘(c) = 2.
(c) The average height of the tree over the time interval 2 ≤ t ≤ 10 is given by \(\frac{1}{10-2}\int_{2}^{10}H(t)dt.\)
\(\frac{1}{8}\int_{2}^{10}H(t)dt\approx \frac{1}{8}\left ( \frac{1.5+2}{2}\cdot 1+\frac{2+6}{2}\cdot 2+\frac{6+11}{2}\cdot 2+\frac{11+15}{2}\cdot 3 \right )\)
\(=\frac{1}{8}(65.75)=\frac{263}{32}\)
The average height of the tree over the time interval 2 ≤ t ≤ 10 is \(\frac{263}{32}\) meters.
(d) G(x) = 50 ⇒ x = 1
\(\frac{d}{dt}(G(x))=\frac{d}{dx}(G(x))\cdot \frac{dx}{dt}=\frac{(1+x)100-100x\cdot 1}{(1+x)^{2}}\cdot \frac{dx}{dt}=\frac{100}{(1+x)^{2}}\cdot \frac{dx}{dt}\)
\(\frac{d}{dt}(G(x))|_{x=1}=\frac{100}{(1+1)^{2}}\cdot 0.03=\frac{3}{4}\)
According to the model, the rate of change of the height of the tree with respect to time when the tree is 50 meters tall is \(\frac{3}{4}\) meter per year.
Question
Let f be the function defined by \(f(x)=\frac{3}{2x^{2}-7x+5}.\)
(a) Find the slope of the line tangent to the graph of f at x = 3.
(b) Find the x-coordinate of each critical point of f in the interval 1 < x < 2.5. Classify each critical point as the location of a relative minimum, a relative maximum, or neither. Justify your answers.
(c) Using the identity that \(\frac{3}{2x^{2}-7x+5}=\frac{2}{2x-5}-\frac{1}{x-1}, evaluate\int_{5}^{\infty }f(x)\) or show that the integral diverges.
(d) Determine whether the series \(\sum_{n=5}^{\infty }\frac{3}{2n^{2}-7n+5}\) converges or diverges. State the conditions of the test used for determining convergence or divergence.
▶️Answer/Explanation
Ans:
(a) \(f'(x)=\frac{-3(4x-7)}{\left ( 2x^{2}-7x+5 \right )^{2}}\)
\(f'(3)=\frac{-3(5)}{\left ( 18-21+5 \right )^{2}}=-\frac{15}{4}\)
(b) \(f'(x)=\frac{-3(4x-7)}{\left ( 2x^{2}-7x+5 \right )^{2}}=0\Rightarrow x=\frac{7}{4}\)
The only critical point in the interval 1 < x < 2.5 has x-coordinate \(\frac{7}{4}.\) f ′ changes sign from positive to negative at \(x=\frac{7}{4}.\) Therefore, f has a relative maximum at \(x=\frac{7}{4}.\)
(c) \(\int_{5}^{\infty }f(x)dx=\lim_{b\rightarrow \infty }\int_{5}^{b}\frac{3}{2x^{2}-7x+5}dx =\lim_{b\rightarrow \infty }\int_{5}^{b}\left ( \frac{2}{2x-5} -\frac{1}{x-1}\right )dx\)
\(=\lim_{b\rightarrow \infty }\left [ In(2x-5)-In(x-1) \right ]_{5}^{b}=\lim_{b\rightarrow \infty }\left [ In\left ( \frac{2x-5}{x-1} \right ) \right ]_{5}^{b}\)
\(=\lim_{b\rightarrow \infty }\left [ In(\frac{2b-5}{b-1})-In(\frac{5}{4}) \right ]=In 2-In\left ( \frac{5}{4} \right )=In\left ( \frac{8}{5} \right )\)
(d) f is continuous, positive, and decreasing on [5, ∞). The series converges by the integral test since \(\int_{5}^{\infty }\frac{3}{2x^{2}-7x+5}dx\) converges.
-OR –
\(\frac{3}{2n^{2}-7n+5}>0 and \frac{1}{n^{2}}>0 for n\geq 5.\)
Since \(\frac{\frac{3}{2n^{2}-7n+5}}{\frac{1}{n^{2}}} =\frac{3}{2}\) and the series \(\sum_{n=5}^{\infty }\frac{1}{n^{2}}\) converges, the series \(\sum_{n=5}^{\infty }\frac{3}{2n^{2}-7n+5}\) converges by the limit comparison test.
Question
| t (minutes) | 0 | 12 | 20 | 24 | 40 |
| v (t) (meters per minute) | 0 | 200 | 240 | -220 | 150 |
Johanna jogs along a straight path. For 0 ≤ t ≤ 40, Johanna’s velocity is given by a differentiable function v. Selected values of v(t), where t is measured in minutes and v(t) is measured in meters per minute, are given in the table above.
(a) Use the data in the table to estimate the value of v'(16).
(b) Using correct units, explain the meaning of the definite integral \(\int_{0}^{40}|v(t)|dt\) in the context of the problem.
Approximate the value of \(\int_{0}^{40}|v(t)|dt\) using a right Riemann sum with the four subintervals indicated in the table.
(c) Bob is riding his bicycle along the same path. For 0 ≤ t ≤ 10, Bob’s velocity is modeled by B(t) = t3 – 6t2 + 300, where t is measured in minutes and B (t) is measured in meters per minute.
Find Bob’s acceleration at time t = 5.
(d) Based on the model B from part (c), find Bob’s average velocity during the interval 0 ≤ t ≤ 10.
▶️Answer/Explanation
Ans:
(a) \(v'(16)\approx \frac{240-200}{20-12}=5 meters/min^{2}\)
(b) \(\int_{0}^{40}|v(t)|dt\) is the total distance Johana jogs, in meters, over the time interval 0 ≤ t ≤ 40 minutes.
\(\int_{0}^{40}|v(t)|dt\approx 12\cdot |v(12)|+8\cdot |v(20)|+4\cdot |v(24)|+16\cdot |v(40)|\)
= 12 · 200+ 8 · 240 + 4 · 220 + 16 · 150
=2400 + 1920 + 880 + 2400
= 7600 meters
(c) Bob’s acceleration is B'(t) = 3t2 – 12t.
B'(5) = 3(25) – 12(5) = 15 meters/min2
(d) Avg vel \(\frac{1}{10}\int_{0}^{10}(t^{3}-6t^{2}+300)dt\)
\(\frac{1}{10}\left [ \frac{t^{4}}{4}-2t^{3}+300t \right ]_{0}^{10}\)
\(\frac{1}{10}\left [ \frac{10000}{4}-2000+3000 \right ]=350 meters/min\)
Question
Grass clippings are placed in a bin, where they decompose. For 0 ≤ t ≤ 30 , the amount of grass clippings remaining in the bin is modeled by A(t) = 6.687 (0.931)t , where A(t) is measured in pounds and t is measured in days.
(a) Find the average rate of change of A(t) over the interval 0 ≤ t ≤ 30. Indicate units of measure.
(b) Find the value of A'(15) . Using correct units, interpret the meaning of the value in the context of the problem.
(c) Find the time t for which the amount of grass clippings in the bin is equal to the average amount of grass clippings in the bin over the interval 0 ≤ t ≤ 30 .
(d) For t >30, L (t), the linear approximation to A at t =30, is a better model for the amount of grass clippings remaining in the bin. Use L (t) to predict the time at which there will be 0.5 pound of grass clippings remaining in the bin. Show the work that leads to your answer.
▶️Answer/Explanation
Ans:
(a) \(\frac{A(30)-A(0)}{30-0}=-0.197 (or-0.196) lbs/day)\)
(b) A'(15) = -0.164 (or – 0.163)
The amount of grass clippings in the bin is decreasing at a rate of 0.164 (or 0.163) lbs/day at time t = 15 days.
(c) \(A(t)=\frac{1}{30}\int_{0}^{30}A(t)dt\Rightarrow t=12.415 (or 12.414)\)
(d) L(t) = A(30) + A'(30) • (t-30)
A'(30) = – 0.055976
A(30) = 0.782928
L(t) = 0.5 ⇒ t = 35.054
Question:
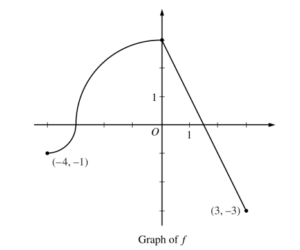
The continuous function f is defined on the interval -4 ≤ x ≤ 3. The graph of f consists of two quarter circles and one line segment, as shown in the figure above. Let \(g(x)=2x+\int_0^x f(t)dt\).
(a) Find g(-3) . Find g'(x) and evaluate g'(-3) .
(b) Determine the x-coordinate of the point at which g has an absolute maximum on the interval -4 ≤ x ≤ 3. Justify your answer.
(c) Find all values of x on the interval -4 ≤ x ≤ 3 for which the graph of g has a point of inflection. Give a reason for your answer.
(d) Find the average rate of change of f on the interval-4 ≤ x ≤ 3. There is no point c, -4 < c < 3, for which f'(c) is equal to that average rate of change. Explain why this statement does not contradict the Mean Value Theorem.
▶️Answer/Explanation
Ans:
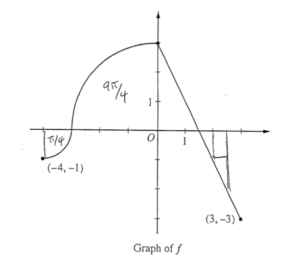
(a)
\(g(-3)=2(-3)+\int_{0}^{-3}f(t)dt = -6 -\frac{9\pi }{4}\)
\(g'(x)=\frac{d}{dx}\left ( 2x + \int_{0}^{x}f(t)dt \right )=2+f(x)\)
g'(-3) = 2 + f(-3) = 2 + 0 = 2
(b)
g'(x) = 0 2 + f(x) = 0
g'(x) f(x) = -2
x = 5/2
\(g(-4)=-8+\int_{0}^{-4}f(t)dt\)
= -8 – 2π
\(g(5/2)= 5+\int^{\frac{5}{2}}_{0} f(t)dt = + \frac{5}{4}\)
\(g(3)= 6+\int_{0}^{3}f(t)dt = 6\)
x = 5/2 , because g’ going from t to – proves it as the only relative maximum and g(5/2) is greater than g at either endpoint.
(c)
f'(x) g”(x) = d/dx (g(x)) = f'(x)
The only point of inflection for g is at x = 0, since f'(x), which is equivalent to g”, only changes signs at x = 0 on the interval -4 ≤ x ≤ 3
(d)
Avg. Rate of change = \(\frac{f(3)-f(-4)}{3-4}\)
\(\frac{-3-1}{3+4}=\frac{-2}{7}\)
Because mean value Theorem only applies when the function is continuous And differentiable on the interval, which doesn’t apply here since f(x) isn’t differentiable at x = 0.
Question:
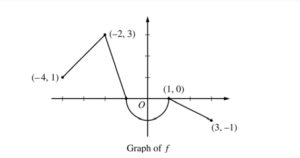
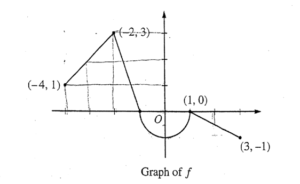
Let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. Let g be the function given by \(g(x)=\int_1^x f(t) dt\).
(a) Find the values of g(2) and g(-2).
(b) For each of g'(-3) and g”(-3) , find the value or state that it does not exist.
(c) Find the x-coordinate of each point at which the graph of g has a horizontal tangent line. For each of these points, determine whether g has a relative minimum, relative maximum, or neither a minimum nor a maximum at the point. Justify your answers.
(d) For -4 < x < 3, find all values of x for which the graph of g has a point of inflection. Explain your reasoning.
▶️Answer/Explanation
Ans:
(a)
\(g(2)= \int_{1}^{2}f(t)dt\)
\(g(2)= \frac{-1}{2}(1)\left ( \frac{1}{2} \right )\)
\(g(2)= -\frac{1}{4}\)
\(g(-2)= \int_{1}^{-2}f(t)dt\)
\(g(-2)= \frac{1}{2}\pi(1)^{2}-\left ( \frac{1}{2}(1)(3) \right )\)
\(g(-2)= \frac{\pi -3}{2}\)
(b)
g'(x) = f(x)
g'(-3) = 2
g”(x) = f'(x)
g”(-3) = 1
(c)
g'(x) = f(x) = 0
x = -1 , 1
At x = -1 g has a relative maximum because g'(x) = f(x) changes from positive to negative at x = 1 g has neither because g'(x) = f(x) does not change sign
(d)
g has inflection points where g”(x) = f'(x) changes sign. This occurs at x = -2 , 0 , 1
Question:
The function f is defined by \(f(x)=\sqrt{25-x^{2}}\) for -5 ≤ x ≤ 5.
(a) Find f'(x).
(b) Write an equation for the line tangent to the graph of f at x = -3.
(c) Let g be the function defined by \(g(x)=\left\{\begin{matrix}
f(x) &for -5\leq x\leq -3 & & \\x+7
&for -3<x\leq 5. & &
\end{matrix}\right.\)
Is g continuous at x = -3 ? Use the definition of continuity to explain your answer
(d) Find the value of \(\int_{0}^{5}x\sqrt{25-x^{2}}dx.\)
▶️Answer/Explanation
Ans:
(a)
\(= (25-x^{2})^{1/2}\)
\(f'(x)=\frac{1.-2x}{2\sqrt{25-x^{2}}}=\frac{-x}{\sqrt{25-x^{2}}}\)
(b)
\(f'(-3)=\frac{3}{\sqrt{25-9}}=\frac{3}{\sqrt{16}}=\frac{3}{4}\) \(f(-3)=\sqrt{25-9}= \sqrt{16}=4\)
\(y = \frac{3}{4}(x+3)+4\)
(c)
\(\lim_{x\rightarrow -3^{-}}g(x)=f(-3)=4\) therefore \(\lim_{x\rightarrow -3}g(x)=4\)
\(\lim_{x\rightarrow -3^{+}}g(x)=-3+7=4\)
g(-3) = f(-3) = 4 \(\lim_{x\rightarrow -3}g(x)\) exists and is equal to g(-3)
g is continuous at x = -3
(d)
u = 25-x2 \(\frac{-1}{2}\int_{25}^{0}4^{1/2}du = \frac{1}{2}\int_{0}^{25}4^{1/2}du = \frac{1}{2}.\frac{24}{3}^{3/2}\int_{0}^{25}\)
\(\frac{-1}{2}du = +2xdx\)
\(= \frac{1}{3}.25^{3/2}=\frac{125}{3}\)
Question:
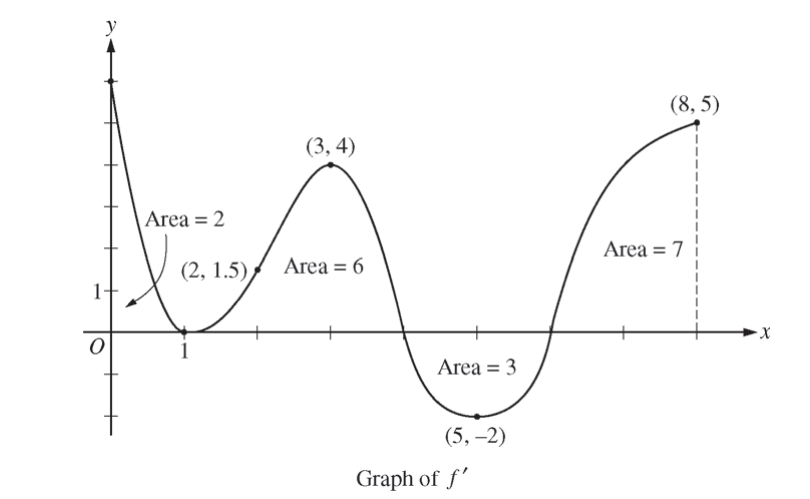
The figure above shows the graph of f’, the derivative of a twice-differentiable function f, on the closed interval 0 ≤ x ≤ 8. The graph of f’ has horizontal tangent lines at x = 1, x = 3, and x = 5. The areas of the regions between the graph of f’ and the x-axis are labeled in the figure. The function f is defined for all real numbers and satisfies f (8) = 4.
(a) Find all values of x on the open interval 0 < x < 8 for which the function f has a local minimum. Justify your answer.
(b) Determine the absolute minimum value of f on the closed interval 0 ≤ x ≤ 8. Justify your answer.
(c) On what open intervals contained in 0 < x < 8 is the graph of f both concave down and increasing? Explain your reasoning.
(d) The function g is defined by \(g(x)=(f(x))^{3}\), if \(f(3)= -\frac{5}{2},\) find the slope of the line tangent to the graph of g at x = 3.
▶️Answer/Explanation
Ans:
(a)
X = 6
f has a local minmum at x = 6, because the graph of f’ changes from negative to positive at x = 6, so using the first derivative test and f has a critical number at x = 6, f has a local minimum
(b)
local minimum = x = 6 f(8) = 4
\(f(6)\rightarrow \int_{6}^{8}f'(x)dx = 7 = f(8)-f(6)=4-f(6)\) f(6) = -3
\(f(0)\rightarrow \int_{0}^{8}f'(x) = 12 = f(8)-f(0)=4-f(0)\) f(0) = -8
The absolute minimum value of f on the interval 0 ≤ x ≤ 8 is -8 because it is the lowest value for the among the endpoints and critical numbers.
(c) \({f}” < 0\)
The open intervals where the graph of f is both concave down and increasing is (0, 1) u (3, 4), or 0 < x < 1 and 3 < x 4, because using the graph of f’, when the graph of f’ is positive and the slope of f’ is negative that means that f is increasing and f” is negative so f is both concave down and increasing.
(d)
g'(x) = 3 (f(x))2. f'(x)
g'(3) = 3 (f(3))2 . f'(3) = 3 (-5/2)2 . (4)
= 3 (25/4)4 = 75
g'(3) = 75
Question:
Grass clippings are placed in a bin, where they decompose. For 0 ≤ t ≤ 30 , the amount of grass clippings remaining in the bin is modeled by A(t) = 6.687 (0.931)t , where A (t) is measured in pounds and t is measured in days.
(a) Find the average rate of change of A (t) over the interval 0 ≤ t ≤ 30 . Indicate units of measure.
(b) Find the value of A'(15) . Using correct units, interpret the meaning of the value in the context of the problem.
(c) Find the time t for which the amount of grass clippings in the bin is equal to the average amount of grass clippings in the bin over the interval 0 ≤ t ≤ 30.
(d) For t > 30, L(t), the linear approximation to A at t = 30, is a better model for the amount of grass clippings remaining in the bin. Use L (t) to predict the time at which there will be 0.5 pound of grass clippings remaining in the bin. Show the work that leads to your answer.
▶️Answer/Explanation
Ans:
(a)
\(\frac{A(30)-A(0)}{30-0}=\frac{-5.904}{30}\approx -.197\frac{pounds}{day}\)
(b)
A'(t) = – .478(.931)t
A'(15) = -.164 \(\frac{pounds}{day}\)
The amount of grass clippings in the bin is decreasing (decomposing) at a rate of .164 pounds per day at time = 15 days
(c)
Average amount \(=\frac{1}{30}\int_{0}^{30}A(t)dt = 2.75263511\)
A(t) = 2.75263511 = 6.687 (.931)t
this occurs at t = 12.414 days
(d)
L(t) is the tangent line to A(t) at t = 30
A(30) = .783 ⇒ (30, .783) = (t, A(t))
A'(30) = -.056 let -.056 = M
(y-y1) = m (x, x1) so for this problem,
(A(t) – .783) = -.056(t-30)
When there are .5 pounds of grass, A(t) = .5,
(.5-.783) = -.056(t-30)
t = 35.054 days
Question:
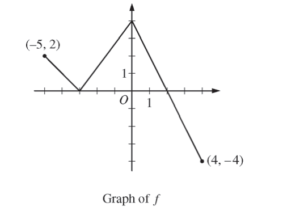
The function f is defined on the closed interval [-5, 4] . The graph of f consists of three line segments and is shown in the figure above. Let g be the function defined by \(g(x)=\int_{-3}^{x}f(t)dt.\)
(a) Find g(3) .
(b) On what open intervals contained in -5 < x < 4 is the graph of g both increasing and concave down? Give a reason for your answer.
(c) The function h is defined by \(h(x)= \frac{g(x)}{5x}\). Find h'(3).
(d) The function p is defined by p(x) = f(x2 – x). Find the slope of the line tangent to the graph of p at the point where x = -1.
▶️Answer/Explanation
Ans:
\(g(x)= \int_{-3}^{3}f(t)dt\)
\(= \frac{1}{2}(5)(4)-\frac{1}{2}(1)(2)\)
= 10 – 1 = 9
(b)
g'(x) > 0 ⇔ f(x) > 0
g”(x) < 0 ⇔ f'(x) < 0
(-5, -3), (0, 2)
(c)
\(h(x)=\frac{g(x)}{5x}\)
\(h'(x)= \frac{(5x)(g'(x))-g(x).5}{25x^{2}}\)
\(h'(3)= \frac{(15)(f(3))-g(3).5}{9.25}=\frac{(15)(-2)-(9)(5)}{9.25}\)
(d)
p(x) = f(x2 – x)
p'(x) = f'(x2-x) . (2x-1)
p'(-1) = f'(1+1) . (-2-1) = f'(2).-3
= (-2) (-3)
= 6
\({f}'(2)=\frac{-4-4}{4-0}=\frac{-8}{4}=-2\)
Question:
The twice-differentiable functions f and g are defined for all real numbers x. Values of f, f’, g, and g’ for various values of x are given in the table above.
(a) Find the x-coordinate of each relative minimum of f on the interval [-2, 3] . Justify your answers.
(b) Explain why there must be a value c, for -1 < c < 1, such that f”(c) =0.
(c) The function h is defined by h(x) = In (f(x)). Find h'(3). Show the computations that lead to your answer.
(d) Evaluate \(\int_{-2}^{3}f'(g(x))g'(x)dx.\)
▶️Answer/Explanation
Ans:
(a)
Critical numbers : x = -1, 1
f has a rel. min. at x = 1 because f'(1) = 0 and f’ switches sign from negative to positive there.
(b)
f'(-1) = 0 and f'(1) = 0, and f'(x) is differentiable and continuous on the internal so by rolle’s Theorem there is some value c where f”(c) = 0.
(c)
\(h'(x)=\frac{f'(x)}{f(x)}\)
\(h'(3)=\frac{f'(3)}{f(3)}\)
\(h'(3)=\frac{\frac{1}{0}}{7}\)
\(h'(3)=\frac{1}{2}\cdot \frac{1}{7}\)
\(h'(3)=\frac{1}{14}\)
(d)
u = g(x)
du = g'(x) dx
\(\int f'(u)du\)
\(\left [ f\left ( g(x) \right ) \right ]_{-2}^{3}\)
\(f(g(3)) – f(g(-2))\)
\(f(1) – f(-1)\)
\(2-8\)
\(-6\)
Question:
Consider the curve given by the equation y3 – xy = 2. It can be shown that \(\frac{dy}{dx}= \frac{y}{3y^{2}-x}.\)
(a) Write an equation for the line tangent to the curve at the point (-1, 1).
(b) Find the coordinates of all points on the curve at which the line tangent to the curve at that point is vertical.
(c) Evaluate \(\frac{d^{2}y}{dx^{2}}\) at the point on the curve where x = -1 and y = 1.
▶️Answer/Explanation
Ans:
(a)
\(Slope = \frac{dy}{dx}@(-1, 1): \frac{1}{3(1)^{2}-(-1)}=\frac{1}{4}\)
Point = ( -1, 1)
\(y – 1 = \frac{1}{4}(x+1)\)
\(y – 1 = \frac{x}{4}+\frac{1}{4}\)
\(y = \frac{x}{4}\times +\frac{5}{4}\)
(b) Vertical tangent line ⇒ slope undefined
⇒ denominator = 0 ⇒ 3y2 – x = 0
3y2 = x
Substitute “x” for “3y2” in the equation of the curve
\(y ^{3}-\left [ 3y^{2}\cdot y \right ]= 2\) y3 – 3y2 = 2
-2y3 = 2
(-1)3 – x•(-1) = 2 Vertical tangents y3 = -1
-1 + x = 2 at (3, 1) y = -1
x = 3
(c)
\(\frac{dy}{dx}@(-1, 1)=\frac{1}{4}\) 3y2 – x = 3-(-1) = 4
\(\frac{d^{2}y}{dx^{2}}=\frac{\left [ y’\cdot (3y^{2}-x) \right ]-\left [ (6yy’ -1)\cdot (y) \right ]}{\left ( 3y^{2}-x \right )^{2}}\)
\(= \frac{\left ( \frac{1}{4}\cdot 4 \right )-\left ( \frac{1}{2}\cdot 1 \right )}{16}=\frac{1-\frac{1}{2}}{16}=\frac{\frac{1}{2}}{16}=\frac{1}{2}\cdot \frac{1}{16}\)
\(=\frac{1}{32}\)
Question:
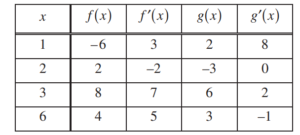
The functions f and g have continuous second derivatives. The table above gives values of the functions and their derivatives at selected values of x.
(a) Let k(x) = f(g(x)). Write an equation for the line tangent to the graph of k at x = 3.
(b) Let \(h(x)=\frac{g(x)}{f(x)}.\) Find h'(1).
(c) Evaluate \(\int_{1}^{3}f”(2x)dx.\)
▶️Answer/Explanation
Ans:
(a)
K(3) = f(g(3))
= f(6)
= 4
k'(x) = f'(g(x)) ·g'(x)
k'(3) = f'(g(3))·g'(3)
= f'(6)·2
= 5.2
= 10
y – 4 = 10 (x-3)
(b)
\(h'(x)=\frac{f(x)g'(x)-g(x)f'(x)}{(f(x))^{2}}\) \(h'(1)=\frac{-2}{2}\)
\(h'(1)=\frac{f(1)g'(1)-g(1)f'(1)}{(f(1))^{2}}\)
\(=\frac{(-6)(8)-(2)(3)}{(-6)^{2}}\)
\(=\frac{-48-6}{36}\)
\(=\frac{-54}{36}\)
(c)
\(\left [ \frac{1}{2}f'(2x) \right ]_{1}^{3}\)
\(\left [ \frac{1}{2}f'(6) \right ]-\left [ \frac{1}{2}f'(2) \right ]\)
\(\frac{5}{2}+1\)
\(\frac{7}{2}\)
Question:
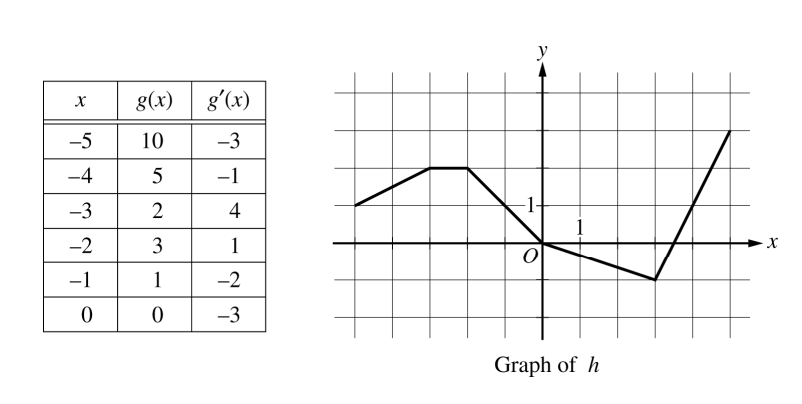
Let f be the function defined by f(x) = cos (2 x) + esin x .
Let g be a differentiable function. The table above gives values of g and its derivative g’ at selected values of x.
Let h be the function whose graph, consisting of five line segments, is shown in the figure above.
(a) Find the slope of the line tangent to the graph of f at x = π.
(b) Let k be the function defined by k(x) = h(f(x)). Find k'(π).
(c) Let m be the function defined by m(x) = g(-2x)•h(x). Find m'(2).
(d) Is there a number c in the closed interval [−5, -3 ] such that g'(c) = −4 ? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\({f}'(x) = -2sin (2x) + e^{sinx} (cos x)\)
\({f}'(π) = -2 sin (2π) + e^{sinx}(cos π)\)
\(= 0 + 1(-1)\)
\(= -1\)

(b)
\({k}'(x) = {h}'(f(x)) ({f}'(x))\)
\({k}'(π) = {h}'(f(π)){ f}'(π)\)
\(= {h}'(2) (-1)\)
\(= 1/3\)
cos (2π) + esinπ
\(1 + 1\)
(c)
In'(x) = [g'(-2x) (-2) •h(x)] + [h'(x)•g(-2x)]
In'(2) = [-2g'(-4)•h(2)] + [h'(2)•g(-4)]
=(2•-2/3) + (-1/3 •5)
\(= -4/3 + -5/3\)
\(= -9/3\)
\(= -3\)
(d)
g(x) = differentiable →g(x) continuous is mean value theorem states that
\({f}'(c)=\frac{f(b)-f(a)}{b-a}\)
\(=\frac{g(-3)-g(-5)}{-3+5}=\frac{2-10}{2}\)
\(= -8/2\)
\(= -4\)
Yes, there’s aa number C is the closed interval such that \({g}'(c) = -4\)
Question:
Let f be the function defined by f(x) = ex cos x.
(a) Find the average rate of change of f on the interval 0 ≤ x ≤ π .
(b) What is the slope of the line tangent to the graph of f at \(x = \frac{3\pi }{2}?\)
(c) Find the absolute minimum value of f on the interval 0 ≤ x ≤ 2π. Justify your answer.
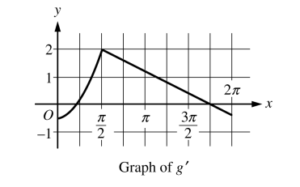
(d) Let g be a differentiable function such that \(g\left ( \frac{\pi }{2} \right )=0.\) The graph of g’, the derivative of g, is shown below. Find the value of \(\lim_{x\rightarrow \pi /2}\frac{f(x)}{g(x)}\) or state that it does not exist. Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(\frac{\int_{0}^{r}f'(x)dx}{r}=\frac{f(r)-f(0)}{r}=\frac{e^{r}cosr-e^{0}cos 0}{r}\)
\(\frac{e^{r}(-1)-1(1)}{r}=\frac{-e^{r}-1}{r}\)
(b)
\(\frac{df}{dx}=e^{x}cos x + e^{x}(-sinx)\)
\(=e^{x}(cos x -sinx)\)
\(=e^{3r/2}(0-(-1))=e^{3r/2}\)
(c)
from part B
\(f'(x)=e^{x}(cos x – sin x)= 0 \rightarrow e^{x}=0\) or cox = sin x \(x = \frac{\pi }{4},\frac{5\pi}{4}\)
Minima either have a derivative at 0, undefined, or are boundary points.
So possible values : x = 0, x = 2π, x = π/4 x = 5π/4
f(x) = 1 f(x) = e2π \(f(x)=e^{\pi /4}\left ( \frac{\sqrt{2}}{2} \right )\) \(f(x)=e^{5\pi /4}\left ( -\frac{\sqrt{2}}{2} \right )\)
Since \(e^{5\pi /4}\left ( -\frac{\sqrt{2}}{2} \right )\) is the only negative value of f(x), the absolute minimum of f(x) on 0 ≤ x ≤ 2π is \(-\frac{\sqrt{2}}{2}e^{5\pi /4}\) .
(d)
Note \(\lim_{x\rightarrow \frac{\pi }{2}}(g(x))=0\) since g(x) is differentiable (and thus continuous), and \(g\left ( \frac{\pi }{2} \right )=0.\) Also \(f\left ( \frac{\pi }{2} \right )=e^{\pi /2}\left ( cos\left ( \frac{\pi }{2} \right ) \right )=e^{\pi /2}(0)=0,\) and f(x) is continuous, So \(\lim_{x\rightarrow \frac{\pi }{2}}f(x)=0.\) So by L’ Hopital’s rule,
\(\lim_{x\rightarrow \frac{\pi }{2}}\left ( \frac{f(x)}{g(x)} \right )=\lim_{x\rightarrow \frac{2 }{2}}\left ( \frac{f'(x)}{g'(x)} \right )=\frac{e^{\pi /2}\left ( cos\frac{\pi }{2}-sin\frac{\pi }{2} \right )}{2}=\frac{-e^{\pi /2}}{2}\)
Question:
Functions f, g, and h are twice-differentiable functions with g(2) = h(2) = 4. The line \(y = 4+\frac{2}{3}(x-2)\) is tangent to both the graph of g at x = 2 and the graph of h at x = 2.
(a) Find h'(2).
(b) Let a be the function given by a(x) = 3x3h(x). Write an expression for a'(x). Find a'(2).
(c) The function h satisfies \(h(x)=\frac{x^{2}-4}{1-(f(x))^{3}}\) for x ≠ 2. It is known that \(\lim_{x\rightarrow 2}h(x)\) can be evaluated using L’Hospital’s Rule. Use \(\lim_{x\rightarrow 2}h(x)\) to find f(2) and f'(2 ). Show the work that leads to your answers.
(d) It is known that g(x) ≤ h(x) for 1 < x < 3. Let k be a function satisfying g(x) ≤ k(x) ≤ h(x) for 1 < x < 3. Is k continuous at x = 2 ? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(y = \frac{2}{3}(x-2)+4\)
point (2, 4) slope 2/3
h'(2) = 2/3
(b)
a'(x) = h'(x).3x3 + 9x2 h(x)
a'(2) = h'(2) . 3(2)3 + 9(2)2 h(2)
\(a'(2)=\frac{2}{3}\cdot 3\cdot 2^{3}+9\cdot 2^{2}\cdot 4\)
(c)
\(\lim_{x\rightarrow 2}\frac{x^{2}-4}{1-(f(x))^{3}}= \lim_{x\rightarrow 2}\frac{2x}{-3(f(x))^{2}.f'(x)}\) h (2) = 4
\(\therefore \lim_{x\rightarrow 2} h(x)\) must equal 4
\(\therefore \lim_{x\rightarrow 2} x^{2}-4=0\)
\( \lim_{x\rightarrow 2} 1-(f(x))^{3}=0\) if f(2) = 1 \(=\frac{2(2)}{-3(1)^{2}\cdot f'(2)}\)
∴ Indeterminate form 0/0 \(=\frac{4}{-3\cdot f'(2)}\) f'(2) must equal -1/3 so that \(\lim_{x\rightarrow 2} h(x) = 4\)
and L’Hopital’s rule applies \(=\frac{4}{-3\cdot -1/3}\)
Such that f(2) = 1 = 4/1
\(\lim_{x\rightarrow 2} h(x) = 4\) such that f(2) = 1 and f'(2) = -1/3
(d)
2 and h given as twice – differentiable ∴ g and h are continuous for 1 < x < 3
g(x) ≤ k(x) ≤ h(x)
\(\lim_{x\rightarrow 2} g(x) = 4\) because g continuous and g(2) = 4
\(\lim_{x\rightarrow 2} h(x) = 4\) because h continuous and h(2) = 4
By squeeze theorem, \(\lim_{x\rightarrow 2} k(x) = 4\)
k is between or equal to g and h for 1 < x < 3, given g(2) = 4 h (2) , meaning k(2) must equal 4, and \(\lim_{x\rightarrow 2} k(x) = 4\) so k(x) is continuous at x = 2
Question:
Consider the function y = f (x) whose curve is given by the equation 2y2 − 6 = y sin x for y > 0.
(a) Show that \(\frac{dy}{dx}=\frac{ycos x}{4y-sin x}.\)
(b) Write an equation for the line tangent to the curve at the point (0, \(\sqrt{3}\) ).
(c) For 0 ≤ x ≤ π and y > 0, find the coordinates of the point where the line tangent to the curve is horizontal.
(d) Determine whether f has a relative minimum, a relative maximum, or neither at the point found in part (c). Justify your answer.
▶️Answer/Explanation
Ans:
(a)
2y2-6 = y sin x
4y y’ = y cos x + y’ sin x
4y y’ – y’ sin x = y cos x
y'(4y-sinx) = y cos x
\(y’ = \frac{ycos x}{4y-sinx}\)
\(\frac{dy}{dx} = \frac{ycos x}{4y-sinx}\)
(b)
\(\frac{dy}{dx}At (0,\sqrt{3})=\frac{\sqrt{3}cos(0)}{4\sqrt{3}-sin(0)}=\frac{\sqrt{3}(1)}{4\sqrt{3}-(0)}=\frac{\sqrt{3}}{4\sqrt{3}}=\frac{1}{4}\)
\(y-\sqrt{3}=\frac{1}{4}(x-0)\)
(c)
2y2 – 6 = y sin x
\(\frac{dy}{dx}=\frac{ycos x}{4y – sinx}\) y ≠0 : -6 = 0 sinx
\(0=\frac{ycos x}{4y – sinx}\)
\(x = \frac{\pi }{2}: 2y^{2}-6=y sin(\frac{\pi }{2})\)
\(2y^{2}-6=y (x)\)
0 = y cos x 2y2 – y-6 =0
y ≠ 0 x ≠ 0 (2y + 3) (y – 2) = 0
Since
0 = y cos x cos (0) = 1 y = 2 2y + 3 = 0
x = π/2 and 2y = -3
0 ≠ 1
f(x) has a horizontal tangent at \(\left ( \frac{\pi }{2},2 \right )\)
(d)
Since \(\frac{d^{2}y}{dx^{2}}<0\) at \(\left ( \frac{\pi }{2},2 \right )\), f has a relative maximum at that point.
\(\frac{dy}{dx}=\frac{y cos x}{4y-sin x}\)
\(\frac{d^{2}y}{dx^{2}} = \frac{(4y-sinx)\left [ y(-sinx)+y’cos x \right ]-(y cos x)(4y’-cosx)}{(4y-sin x)^{2}}\)
At \(\left ( \frac{\pi }{2},2 \right )\) : \(\frac{d^{2}y}{dx^{2}} = \frac{(4.2-1)\left [ 2(-1)+0 cos x \right ]-(2(0))(4(0)-0)}{(4(2)-1)^{2}}\)
\(\frac{d^{2}y}{dx^{2}} = \frac{(8-1)(-2)}{(8-1)^{2}}=\frac{7(-2)}{7}=\frac{-2}{7}\)
concave down
Question
Let f, g, and h be differentiable functions.
(A) Find a general formula for \((\frac{fg}{h}){}’\)
(B) Use your formula from part (a) to find \(\left ( \frac{e^{x}\sin (x)}{x^{2}} \right ){}’\)
▶️Answer/Explanation
(A)\(\left ( \frac{fg}{h} \right ){}’=\frac{(fg){}’h-fgh{}’}{h^{2}}=\frac{(f{g+fg{}’})h-fgh{}’}{h^{2}}\)
(B)\(\frac{(e^{x}\sin x+e^{x}\cos x)x^{2}-e^{x}\sin x(2x)}{x^{4}}=\frac{xe^{x}(\sin x+\cos x)-2\sin x}{x^{3}}=\frac{e^{x}((x-2)\sin x)+x\cos x}{x^{3}}\)`
Question
A curve is defined by the equation \(y=x^{3}-4\).
(A) Find the slope of the tangent to the curve at point (2, 4).
(B) Find the slope of the normal line at point (2, 4).
(C) Write an equation for the normal line.
▶️Answer/Explanation
(A) The slope of the tangent,\(m_{tangent}\), is defined as \(\frac{\mathrm{d} y}{\mathrm{d} x}.\frac{\mathrm{d} y}{\mathrm{d} x}=3x^{2}\).At \(x=2,\frac{\mathrm{d} y}{\mathrm{d} x}=12.\)
(B)\(m_{normal}=-\frac{1}{m_{tangent}}=-\frac{1}{3x^{2}}=-\frac{1}{12}\) at x=2.
(C) Since the slope of the normal line is \(-\frac{1}{12}\), if we take the point (2, 4), we can write \(\frac{y-4}{x-2}=-\frac{1}{12}\) or \(y=-\frac{1}{12}x+4\frac{1}{6}\).
Question
The slope of a function f (x) at any point (x, y) is \(\frac{x-3}{x^{2}-3x-4}\) The point \(\left ( 5,\frac{4}{5}\ln 6 \right )\) is on the graph of f (x).
(A) Write an equation of the tangent line to the graph of f (x) at x = 5.
(B) Use the tangent line in part (a) to approximate f (4.5) to the nearest thousandth.
(C) Find the antiderivative of \(\frac{\mathrm{d} f}{\mathrm{d} x}=\frac{x-3}{x^{2}-3x-4}\) with the condition \(f(5)=\frac{4}{5}\ln 6\).
(D) Use the result of part (c) to find f (4.5) to the nearest thousandth.
▶️Answer/Explanation
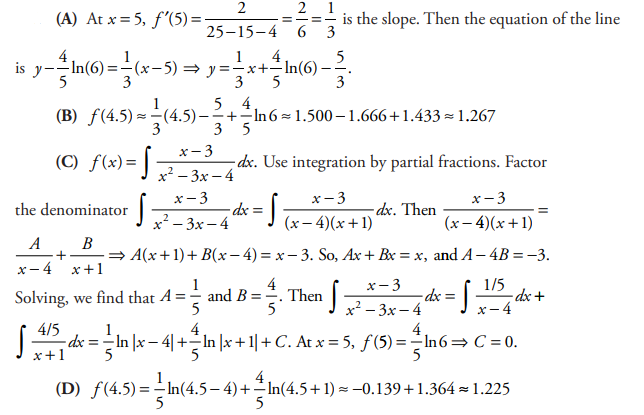
Question
Let f be the function given by \(f(x)=\frac{\sin ^{2}(x)}{x}\).
(A) Find the derivative of f (x).
(B) Write an equation for the tangent line at \(x=\frac{\pi }{2}\).
▶️Answer/Explanation
(A)\(f'(x)=\frac{2x\sin x\cos x-\sin ^{2}x}{x^{2}}=\frac{\sin x(2x\cos x-\sin x)}{x^{2}}\)
(B) At \(x=\frac{\pi }{2},f\left ( \frac{\pi }{2} \right )=\frac{2}{\pi }\),while\( f’\left ( \frac{\pi }{2} \right )=-\frac{4}{\pi ^{2}}\).Using the point-slope formula:\(y-\frac{2 }{\pi }=-\frac{4}{\pi ^{2}}\left ( x-\frac{\pi }{2} \right ) y=-\frac{4}{\pi ^{2}}x+\frac{4}{\pi }\)
Question
This problem is solved without a calculator. The slope of a function f at any given point (x, y) is \(\frac{2y}{3x^{2}}\) . The point (3, 4) is on the graph of f.
(A) Write an equation of the tangent line to the graph of f at x = 3.
(B) Use the tangent line in part (a) to approximate f (5). Is this approximation an overestimate or underestimate? Justify your answer using the second derivative test.
(C) Solve the separable differential equation \( \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2y}{3x^{2}}\) with initial condition f(3) = 4.
(D) Use the solution in part (c) to find f(5).
▶️Answer/Explanation
(A) The slope at x=3 (i.e.,the point (3,4)) is
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2y}{3x^{2}}\Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2(4)}{3(3)^{2}}=\frac{8}{27}\)
Now write the equation of the tangent line at (3, 4) in point-slope form.
\(y-y_{0}=m(x-x_{0})\Rightarrow y-4=\frac{8}{27}(x-3)\Rightarrow y=\frac{8}{27}(x-3)+4\Rightarrow y=\frac{8}{27}x+\frac{28}{9}\)
(B)\(f(5)=\frac{8}{27}(5-3)+4=\frac{124}{27}\) This is an overestimate because the graph is concavedown over the interval (3,5) with a negative second derivative of \(\left ( (3x^{2})y’-6x(2y) \right )/(3x^{2})^{2}\)
(C) Start by separating the variables and integrating both sides
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2y}{3x^{2}}\Rightarrow \frac{1}{2y}dy=\frac{1}{3x^{2}}dx\Rightarrow \int \frac{1}{2y}dy=\int \frac{1}{3x^{2}}dx
\frac{1}{2}\int \frac{1}{y}dy=\frac{1}{3}\int x^{-2}dx\Rightarrow \frac{1}{2}\ln |y|=\left ( \frac{1}{3} \right )\frac{x^{-1}}{-1}+c_{1}\Rightarrow \frac{1}{2}\ln \left | y \right |=-\frac{1}{3x}+c_{1}
\ln \left | y \right |=-\frac{2}{3x}+c_{2}\Rightarrow e^{\ln \left | y \right |}=e^{-\frac{2}{3x}+c_{2}}=e^{-\frac{2}{3x}.e^{c_{2}}}\)
\(y=c_{3}e^{-\frac{2}{3x}}\)
Now use the initial condition f(3) = 4 to solve for \(c_{3}\).
\(4=c_{3}e^{-\frac{2}{3(3)}}\Rightarrow c_{3}=4.9954\)
\(y=4.9954e^{-\frac{2}{3x}}\)
(D) Evaluate the equation in C at f(5).
\(f(5)=4.9954e^{-\frac{2}{3(5)}}\approx 4.37184\)