Question
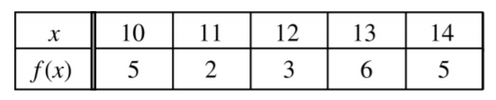
The table above gives values of the continuous function f at selected values of x. If f has exactly two critical points on the open interval (10, 14), which of the following must be true?
A f(x) > 0 for all x in the open interval (10, 14).
B f ‘(x) exists for all x in the open interval (10, 14 ).
C f ‘(x) < 0 for all x in the open interval (10, 11).
D f ‘(12) ≠ 0
Answer/Explanation
Question
\(f(x)=1+x^{\frac{2}{3}}\) , which of the following is NOT true?
(A) f is continuous for all real numbers.
(B) f has a minimum at x = 0 .
(C) f is increasing for x > 0 .
(D) f ′( x) exists for all x.
(E) f ′′(x ) is negative for x > 0 .
Answer/Explanation
Ans:D
Question
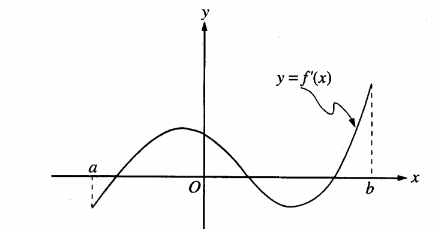
The graph of \(f ′\) , the derivative of f , is shown in the figure above. Which of the following describes all relative extrema of f on the open interval (a b,)?
(A) One relative maximum and two relative minima
(B) Two relative maxima and one relative minimum
(C) Three relative maxima and one relative minimum
(D) One relative maximum and three relative minima
(E) Three relative maxima and two relative minima
Answer/Explanation
Question
Let g be a continuous function on the closed interval [0,1]. Let (0)= 1 and g (1) =0 . Which of the following is NOT necessarily true?
(A) There exists a number h in [0,1] such that \(g(h)\geq g(x) \)for all x in [0,1].
(B) For all a and b in [0,1], if a =b , then g(a)=g(b).
(C) There exists a number h in [0,1] such that \(g(h)=\frac{1}{2}\)
(D) There exists a number h in [0,1] such that \(g(h)=\frac{3}{2}\)
(E) For all h in the open interval \((0,1),\lim_{x\rightarrow h}g(x)=g(h)\)
Answer/Explanation
Ans:D
