Question
Consider the differential equation \(\frac{dy}{dx}=\frac{y^{2}}{x-1}.\)
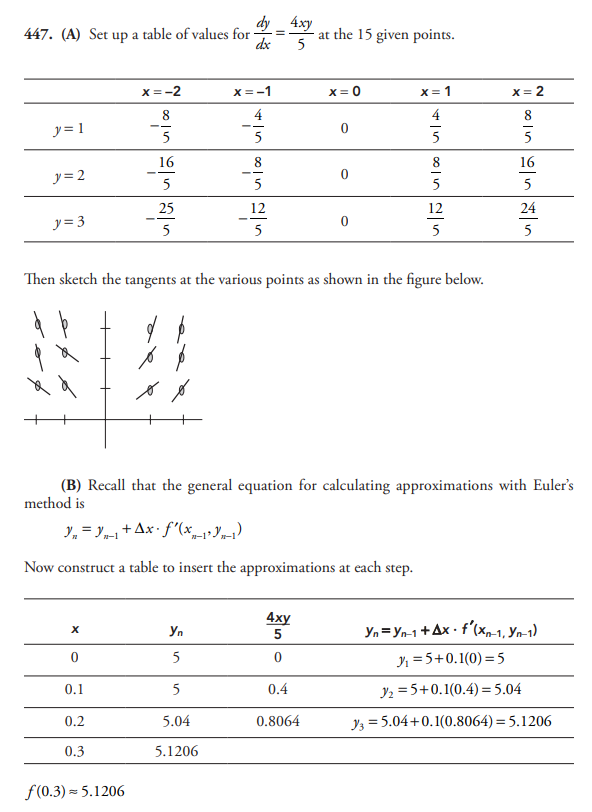
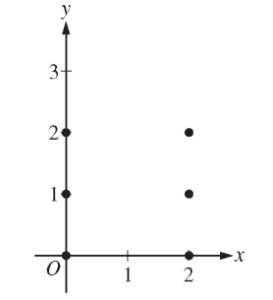
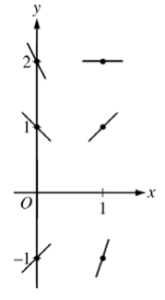
(a) On the axes provided, sketch a slope field for the given differential equation at the six points indicated.
(b) Let y = f(x) be the particular solution to the given differential equation with the initial condition f(x) = 3. Write an equation for the line tangent to the graph of y=f(x) at x= 2.
Use your equation to approximate f(2.1).
(c) Find the particular solution y = f (x) to the given differential equation with the initial condition f (2) = 3.
Answer/Explanation
Ans:
(a) 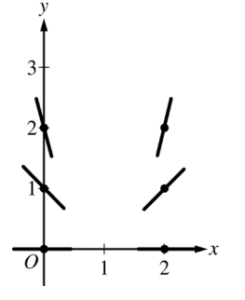
(b) \(\frac{dy}{dx}_{(x,y)=(2,3)}=\frac{3^{2}}{2-1}=9\)
An equation for the tangent line is y = 9(x – 2) + 3.
f(2.1) ≈ 9(2.1-2) + 3 = 3.9
(c) \(\frac{1}{y^{2}}dy=\frac{1}{x-1}dx\)
\(\int \frac{1}{y^{2}}dy=\int \frac{1}{x-1}dx\)
\(-\frac{1}{y}= ln|x-1|+C\)
\(-\frac{1}{3}= ln|2-1|+C\Rightarrow C=-\frac{1}{3}\)
\(-\frac{1}{y}= ln|x-1|-\frac{1}{3}\)
\(y= \frac{1}{\frac{1}{3}-ln(x-1)}\)
Note: This solution is valid for 1 < x < 1 + e1/3.
Question
Consider the differential equation \(\frac{dy}{dx}=2x – y.\)
(a) On the axes provided, sketch a slope field for the given differential equation at the six points indicated.
(b) Find \(\frac{d^{2}y}{dx^{2}}\) in terms of x and y. Determine the concavity of all solution curves for the given differential equation in Quadrant II. Give a reason for your answer.
(c) Let y = f(x) be the particular solution to the differential equation with the initial condition f(2) = 3. Does f have a relative minimum, a relative maximum, or neither at x =2 ? Justify your answer.
(d) Find the values of the constants m and b for which y = mx + b is a solution to the differential equation.
Answer/Explanation
Ans:
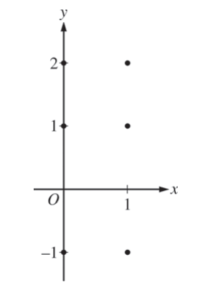
(a) Slopes where x = 0
slopes where x = 1
(b) \(\frac{d^{2}y}{dx^{2}}= 2 – \frac{dy}{dx}= 2 -(2x-y)=2-2x+y\)
In Quadrant II, x < 0 and y > 0, so 2 – 2x + y > 0. Therefore, all solution curves are concave up in Quadrant II.
(c) \(\frac{dy}{dx}|_{(x,y)=(2,3)}=2(2)-3 = 1\neq 0\)
Therefore, f has neither a relative minimum nor a relative maximum at x = 2.
(d) \(y = mx + b \Rightarrow \frac{dy}{dx}=\frac{d}{dx}(mx + b)=m\)
2x – y = m
2x – (mx + b) = m
(2 – m)x – (m + b) = 0
2 – m = 0 ⇒ m = 2
b = -m ⇒ b = -2
Therefore, m = 2 and b = -2.
Question
Consider the differential equation given by \(dy/dx=\frac{4xy}{5}\) .
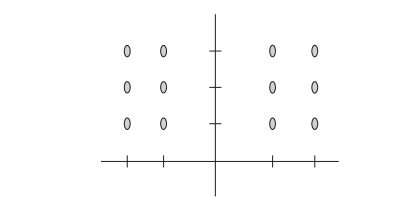
(A) On the axis provided below, sketch a slope field for the given differential equation at the points indicated.
(B) Let y = f (x) be the particular solution to the given differential equation with initial condition f (0) = 5. Use Euler’s method and a step size of 0.1 to approximate f (0.3). Show the work that leads to your answer.
(C) Find the particular solution y = f (x) to the given differential equation with initial condition f (0) = 5.
(D) Use your solution above to find f (0.3).
Answer/Explanation