Question
A function
satisfies 
.Which of the following could be the graph of
A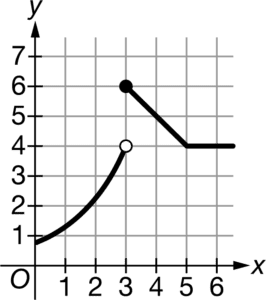 
B 
C
D
Answer/Explanation
Ans:C
In this graph, the values of
approach 6 as
approaches 3 from the left and as x approaches 3 from the right; that is 
Since the one-sided limits have the common value 6,
Question
Let f be the function given by \(f(x)=\frac{e^{3x}-1}{x}\) for
. Which of the following equations expresses the property that f(x) can be made arbitrarily close to 3 by taking x
sufficiently close to 0, but not equal to 0 ?
A f(0)=3
B 
C 
D 
Answer/Explanation
Ans:C
This is the correct notation that the limit of f(x
is 3 as x approaches 0 (but is not equal to 0 where
Question
The function
has the property that as
gets closer and closer to 3, the values of
get closer and closer to 5. Which of the following statements must be true?
A f(3)=5
B f(5)=3
C 
D 
Answer/Explanation
Ans:C
The given information about the function f
is a good, informal description of the mathematical statement
Question
The function
has the property that as
gets closer and closer to 3, the values of
get closer and closer to 5. Which of the following statements must be true?
A f(3)=5
B f(5)=3
C
D
Answer/Explanation
Ans:C
The given information about the function f
is a good, informal description of the mathematical statement
Question
Let f (x)=3x+1 for all real x and let ε > 0 . For which of the following choices of δ is \(|f(x)-7|<\varepsilon\) whenever \(|x-2|<\delta \)?
(A)\(\frac{\varepsilon }{4} \)
(B)\(\frac{2}{ε}\)
(C) \(\frac{ε}{ε +1}\)
(D) \(\frac{ε +1}{ε}\)
(E) 3ε
Answer/Explanation
Ans:A