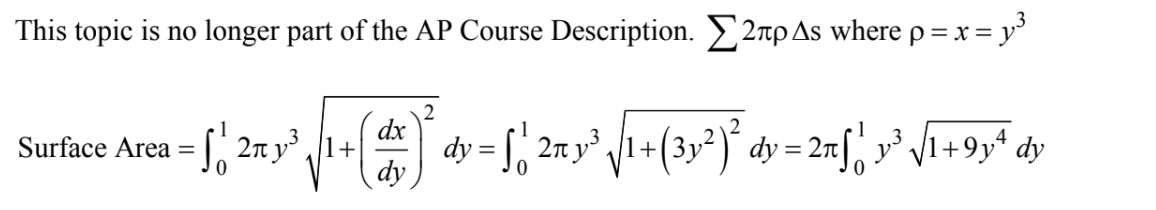Question
A region in the plane is bounded by the graph of \(y=\frac{1}{x}\) , the x-axis, the line x = m , and the line x = 2m , m > 0 . The area of this region
(A) is independent of m .
(B) increases as m increases.
(C) decreases as m increases.
(D) decreases as m increases when \(m<\frac{1}{2}\), increases as m increases when\( m>\frac{1}{2}\).
(E) increases as m increases when \(m<\frac{1}{2}\); decreases as m increases when \(m<\frac{1}{2}\).
Answer/Explanation
Question
The area of the region bounded by the lines x=0,x=2 and y = 0 and the curve \(y=e^{x/2}\) is
(A)\(\frac{e-1}{2}\) (B) e −1 (C) 2 (e −1 ) (D) 2 e −1 (E) 2e
Answer/Explanation
Ans:C
Question
Which of the following gives the area of the surface generated by revolving about the y-axis the arc of\( x = y^{3}\) from y = 0 to y = 1?
(A)\(2\pi \int_{0}^{1}y^{3}\sqrt{1+9y^{4}}dy\)
(B)\(2\pi \int_{0}^{1}y^{3}\sqrt{1+y^{6}}dy\)
(C)\(2\pi \int_{0}^{1}y^{3}\sqrt{1+3y^{4}}dy\)
(D)\(2\pi \int_{0}^{1}y\sqrt{1+9y^{4}}dy\)
(E)\(2\pi \int_{0}^{1}y\sqrt{1+y^{6}}dy\)
Answer/Explanation
Ans:A