Question
If the power series \(∑_{n=0}^{∞}a_n(x−4)^n\) converges at x= 7 and diverges at x= 9, which of the following must be true?
I. The series converges at \(x= 1\).
II. The series converges at \(x= 2\).
III. The series diverges at \(x= −1\).
A I only
B II only
C I and II only
D II and III only
Answer/Explanation
Question
The complete interval of convergence of the series \(\sum_{k=1}^{\infty }\frac{(x+1)^{k}}{k^{2}}\) is
(A) 0 < x< 2 (B) 0 ≤ 2 ≤ x (C) −2 < 0 ≤x (D) −2 ≤ x < 0 (E) −2 ≤0 ≤x
Answer/Explanation
Ans:E
The ratio test shows that the series is convergent for any value of x that makes|x+1|<1 The solutions to |x+1|=1 are the endpoints of the interval of convergence. Test x = −2 and x = 0 in the series. The resulting series are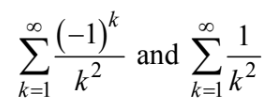 
which are both convergent. The interval is 
Question
Which of the following is equal to the area of the region inside the polar curve r = 2cos θ and outside the polar curve r = cos θ ?
(A)\(3\int_{0}^{\frac{\pi}{2}}cos^{2}\Theta d\Theta\) (B)\(3\int_{0}^{\pi}cos^{2}\Theta d\Theta\) (C)\(\frac{3}{2}\int_{0}^{\frac{\pi}{2}}cos^{2}\Theta d\Theta\) (D)\(3\int_{0}^{\pi}cos\Theta d\Theta\) (E)\(3\frac{0}{\pi}cos\Theta d\Theta\)
Answer/Explanation
Ans:A
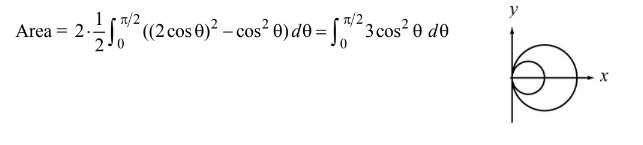
Question
The Taylor series for a function f about x=0 converges to f for The nth-degree
Taylor polynomial for f about x=0 is given by \( p_{n}(x)=\sum_{k=1}^{n}(-1)^{k}\frac{x^{k}}{k^{2}+k+1} \)Of the following,which is the smallest number for which the alternating series error bound guarantees that
(A)\(\frac{1}{5!}.\frac{1}{31}\)
(B)\(\frac{1}{4!}.\frac{1 }{21}\)
(C)\(\frac{1}{31}\)
(D)\(\frac{1}{21}\)