Question
If n is a non-negative integer, then \(\int_{0}^{1}x^{n}dx=\int_{0}^{1}(1-x)^{n}dx\) for
(A) no n (B) n even, only (C) n odd, only (D) nonzero n, only (E) all n
Answer/Explanation
Ans:E

Question
The marginal profit of manufacturing and selling a flu vaccine is given by P ′(x ) = 1000-0.4x, where x is the number of units of vaccine sold. How much profit should the company expect if it sells 20,000 units of this vaccine?
(A) 12,000,000
(B) 1,200,000
(C) 120,000
(D) 12,000
Answer/Explanation
Ans:(A)
Marginal profit is the derivative of profit.Profit=\(\int_{0}^{20,000}(1,000-0.04x)dx\)
Question
The marginal cost of producing x units of sneakers is C ′( x) =5 +0.4x. Find the cost of producing the first 100 pairs of sneakers.
(A) 2,500
(B) 25,000
(C) 250
(D) 80
Answer/Explanation
Ans:(A)
Marginal cost is the derivative of cost.Cost\(=\int_{0}^{100}(5+0.4x)dx\)
Question
Graphs of the marginal cost and marginal revenue are shown below.Estimate the profit for the first 50 units.
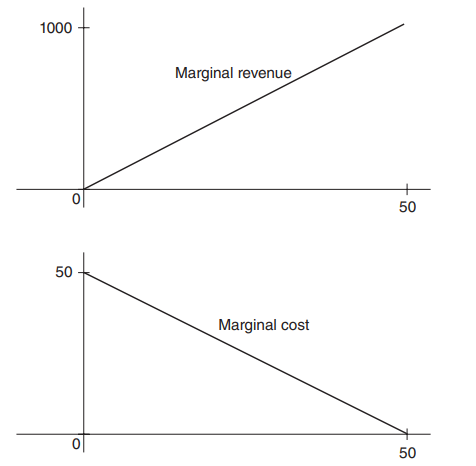
(A) 0
(B) -26,250
(C) 26,250
(D) 23,750
Answer/Explanation
Ans:(D)
Profit = revenue – cost
Revenue= ∫(marginal revenue)
Cost =∫(marginal cost)
To find the revenue and the cost, calculate the area under the graphs of marginal revenue and marginal cost, respectively.
