Question
Topic: Uncertainties and errors
Given: A student is verifying the equation
$$
x=\frac{2 \lambda Y}{Z}
$$
The percentage uncertainties are:
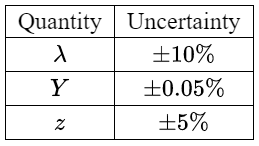
Calculate: the percentage uncertainty in $x$ ?
A. $5 \%$
B. $15 \%$
C. $25 \%$
D. $30 \%$
▶️Answer/Explanation
Ans:B
Solution:
From Formula Booklet:
If: $y=\frac{a b}{c}$ then: $\frac{\Delta y}{y}=\frac{\Delta a}{a}+\frac{\Delta b}{b}+\frac{\Delta c}{c}$
So,
$\frac{\Delta x}{x}=\frac{\Delta \lambda }{\lambda }+\frac{\Delta Y}{Y}+\frac{\Delta Z}{Z}$
Hence percentage uncertainty in $x=10+5+0.05=15 \%$
Question
Topic: Measurements
Given: A student models the relationship between the pressure $p$ of a gas and its temperature $T$ as $p=x+y T$ The units of $p$ are pascal and the units of $T$ are kelvin.
Discuss: the fundamental SI units of $x$ and $y ?$

▶️Answer/Explanation
Ans:A
Solution:
The unit of $x$ can be found by analyzing the given relationship: $p=x+yT$. Since $p$ has units of pascal and $T$ has units of kelvin, the units of $x$ must be such that it cancels out the units of $T$ and leaves behind the units of $p$. Therefore, the units of $x$ are kg m$^{-1}$ s$^{-2}$, which is equivalent to pascal (Pa).
The unit of $y$ can be found by rearranging the given relationship: $p=x+yT \Rightarrow y = \frac{p}{T}$. The units of $y$ can be obtained by dividing the units of $p$ (kg m$^{-1}$ s$^{-2}$) by the units of $T$ (K). This gives units of kg m$^{-1}$ s$^{-2}$ K$^{-1}$, which is equivalent to pascal per kelvin (Pa/K).
Question
Topic: Motion
Given: A sky diver is falling at terminal speed when she opens her parachute.
Discuss: are the direction of her velocity vector and the direction of her acceleration vector before she reaches the new terminal speed?
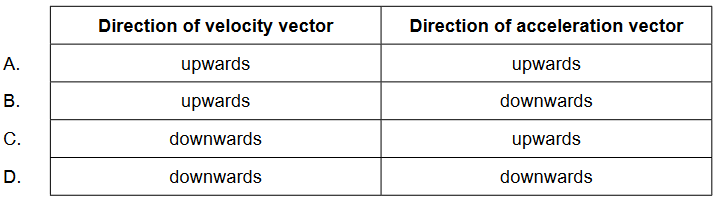
▶️Answer/Explanation
Ans: C
Solution:
The answer is C, downwards for the direction of velocity vector and upwards for the direction of acceleration vector.
When a sky diver is falling at terminal speed, the upward drag force acting on the diver balances the downward force of gravity, resulting in zero net force and a constant velocity. When the diver opens the parachute, the surface area increases and the drag force increases, while the weight of the diver remains the same. This results in a net upward force and an upward acceleration.
Initially, before reaching the new terminal speed, the diver will be falling downwards with a constant velocity. At this point, the direction of the velocity vector is downwards, as this is the direction in which the diver is moving. However, the net force acting on the diver is upwards (due to the drag force being greater than the weight of the diver), and so the direction of the acceleration vector is upwards.
Therefore, the correct answer is downwards for the direction of velocity vector and upwards for the direction of acceleration vector.
Question
Topic: Motion
Given: A stone is thrown downwards from the edge of a cliff with a speed of $5.0 \mathrm{~m} \mathrm{~s}^{-1}$. It hits the ground 2.0 s later.
Calculate: the height of the cliff?
A. $20 \mathrm{~m}$
B. $30 \mathrm{~m}$
C. $40 \mathrm{~m}$
D. $50 \mathrm{~m}$
▶️Answer/Explanation
Ans:B
Solution:
We can use the kinematic equation:
$$
h = v_i t + \frac{1}{2}gt^2
$$
where $h$ is the height of the cliff, $v_i$ is the initial velocity of the stone (which is downwards, so $v_i = -5.0~\mathrm{m/s}$), $g$ is the acceleration due to gravity (which is $10~\mathrm{m/s^2}$ downwards), and $t$ is the time it takes for the stone to hit the ground (which is $2.0~\mathrm{s}$).
Substituting the values we get: (taking downward direction is negative)
$$
\begin{aligned}
-h &= v_i t + \frac{1}{2}gt^2 \\
&= (-5.0~\mathrm{m/s})(2.0~\mathrm{s}) + \frac{1}{2}(-10~\mathrm{m/s^2})(2.0~\mathrm{s})^2 \\
&= 10.0~\mathrm{m} + 20.0~\mathrm{m} \\
&= 30.0~\mathrm{m}
\end{aligned}
$$
Therefore, the height of the cliff is $30.0~\mathrm{m}$.
Question
Topic: Motion
Given: A ball is thrown upwards at an angle to the horizontal. Air resistance is negligible.
Discuss: statement about the motion of the ball is correct?
A. The acceleration of the ball changes during its flight.
B. The velocity of the ball changes during its flight.
C. The acceleration of the ball is zero at the highest point.
D. The velocity of the ball is zero at the highest point.
▶️Answer/Explanation
Ans:B
Solution:
The correct statement about the motion of the ball is (B) The velocity of the ball changes during its flight.
When a ball is thrown upwards at an angle to the horizontal, it experiences a vertical acceleration due to gravity of $g = 9.8~\mathrm{m/s^2}$ downwards, and a horizontal acceleration of zero (assuming air resistance is negligible). The vertical acceleration remains constant throughout the motion of the ball, but the direction of the velocity changes.
Initially, the ball moves upwards with a positive velocity, which decreases due to the acceleration of gravity until the velocity becomes zero at the highest point. After that, the ball starts moving downwards with a negative velocity, which increases due to the acceleration of gravity until it reaches its initial height, where the velocity becomes zero again. Therefore, the velocity of the ball changes during its flight.
On the other hand, statement (A) is incorrect because the acceleration of the ball remains constant during its flight, while statement (C) is incorrect because the acceleration of the ball is never zero. Finally, statement (D) is incorrect because the only horizontal velocity of the ball is zero during its flight (at the highest point).
