Question
Topic: Uncertainties and errors
Given: A student measures the radius $R$ of a circular plate to determine its area. The absolute uncertainty in $R$ is $\Delta R$.
Calculate: the fractional uncertainty in the area of the plate?
A. $\frac{2 \Delta R}{R}$
B. $\left(\frac{\Delta R}{R}\right)^2$
C. $\frac{2 \pi \Delta R}{R}$
D. $\pi\left(\frac{\Delta R}{R}\right)^2$
▶️Answer/Explanation
Ans:A
Solution:
The area of a circle is given by $A = \pi R^2$. We can use the rules of error propagation to determine the fractional uncertainty in the area of the plate.
First, we can find the absolute uncertainty in the area of the plate as follows:
$$
\Delta A = \left|\frac{\partial A}{\partial R}\right|\Delta R = 2\pi R\Delta R
$$
where $\left|\frac{\partial A}{\partial R}\right|$ is the absolute value of the derivative of $A$ with respect to $R$. We can then find the fractional uncertainty in the area of the plate by dividing $\Delta A$ by the nominal value of $A$:
$$
\frac{\Delta A}{A} = \frac{2\pi R\Delta R}{\pi R^2} = \frac{2\Delta R}{R}
$$
Therefore, the answer is (A) $\frac{2\Delta R}{R}$.
Question
Topic: Uncertainties and errors
Given: A proton has momentum $10^{-20} \mathrm{~N} \mathrm{~s}$ and the uncertainty in the position of the proton is $10^{-10} \mathrm{~m}$.
Calculate: the minimum fractional uncertainty in the momentum of this proton?
A. $5 \times 10^{-25}$
B. $5 \times 10^{-15}$
C. $5 \times 10^{-5}$
D. $2 \times 10^4$
▶️Answer/Explanation
Ans:C
Solution:
The Heisenberg uncertainty principle states that the product of the uncertainties in the position and momentum of a particle is bounded from below by a constant, $\hbar/2$:
$$
\Delta x \Delta p \geq \frac{\hbar}{2}
$$
where $\Delta x$ is the uncertainty in position, $\Delta p$ is the uncertainty in momentum, and $\hbar$ is the reduced Planck constant.
We can rearrange this inequality to solve for the minimum fractional uncertainty in the momentum:
$$
\frac{\Delta p}{p} \geq \frac{\hbar}{2p\Delta x}
$$
Substituting the given values, we have:
$$
\frac{\Delta p}{p} \geq \frac{\hbar}{2p\Delta x} = \frac{(6.626 \times 10^{-34} \mathrm{~J \cdot s})/2\pi}{2( 10^{-20} \mathrm{~kg})(10^{-10} \mathrm{~m})} \approx 5 \times 10^{-5}
$$
Therefore, the answer is (c) $5 \times 10^{-5}$.
Question
Topic: Motion
Given: A boy throws a ball horizontally at a speed of $15 \mathrm{~m} \mathrm{~s}^{-1}$ from the top of a cliff that is $80 \mathrm{~m}$ above the surface of the sea. Air resistance is negligible.
Calculate: the distance from the bottom of the cliff to the point where the ball lands in the sea?
A. $45 \mathrm{~m}$
B. $60 \mathrm{~m}$
C. $80 \mathrm{~m}$
D. $240 \mathrm{~m}$
▶️Answer/Explanation
Ans: B
Solution:
We can use the equations of motion to determine the distance from the bottom of the cliff to the point where the ball lands in the sea. Since the initial velocity of the ball is purely horizontal, the horizontal component of the velocity remains constant throughout the motion. The vertical motion of the ball is given by:
$$
y = y_0 + v_{0y} t – \frac{1}{2}gt^2
$$
where $y$ is the vertical displacement, $y_0$ is the initial vertical displacement, $v_{0y}$ is the initial vertical velocity, $g$ is the acceleration due to gravity, and $t$ is time. At the instant the ball hits the water, $y = -80\text{ m}$ and $v_{0y} = 0$, so we have:
$$
-80 \mathrm{~m} = 0 + 0 \cdot t – \frac{1}{2}gt^2
$$
Solving for $t$, we get:
$$
t = \sqrt{\frac{2y_0}{g}} = \sqrt{\frac{2 \cdot 80 \mathrm{~m}}{9.81 \mathrm{~m} \mathrm{~s}^{-2}}} \approx 4.04 \mathrm{~s}
$$
The horizontal distance traveled by the ball is given by:
$$
x = v_{0x} t
$$
where $v_{0x}$ is the initial horizontal velocity. Since the horizontal component of the velocity is constant, we have:
$$
v_{0x} = 15 \mathrm{~m} \mathrm{~s}^{-1}
$$
Therefore, the distance from the bottom of the cliff to the point where the ball lands in the sea is:
$$
x = v_{0x} t = 15 \mathrm{~m} \mathrm{~s}^{-1} \cdot 4.04 \mathrm{~s} \approx 60 \mathrm{~m}
$$
Thus, the answer is (B) $60 \mathrm{~m}$.
Question
Topic: Forces
Given: A book is at rest on a table.
Discuss: What is a pair of action-reaction forces for this situation according to Newton’s third law of motion?
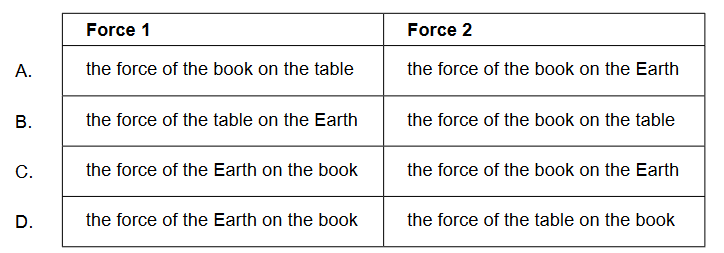
▶️Answer/Explanation
Ans:C
Solution:
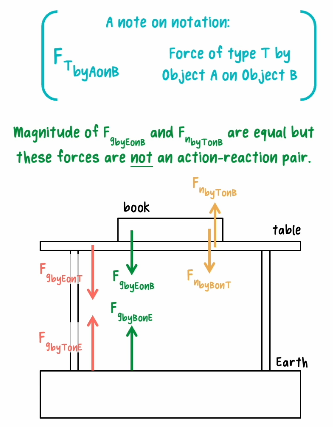
the force of the Earth on the book \& the force of the book on the Earth
Newton’s Third Law:
If object $A$ applies a force on object $B$, then object $B$ applies a force equal in magnitude and opposite in direction on object $A$
The Earth exerts a gravitational force on the table.
The table exerts an equal gravitational force on the Earth.
The Earth exerts a gravitational force on the book.
The book exerts an equal gravitational force on the Earth.
The table exerts a normal force on the book.
The book exerts an equal normal force on the table.
Question
Topic: Work, energy and power
Given: An object has a weight of $6.10 \times 10^2 \mathrm{~N}$.
Calculate: the change in gravitational potential energy of the object when it moves through $8.0 \mathrm{~m}$ vertically?
A. $5 \mathrm{~kJ}$
B. $4.9 \mathrm{~kJ}$
C. $4.88 \mathrm{~kJ}$
D. $4.880 \mathrm{~kJ}$
▶️Answer/Explanation
Ans:B
Solution:
The change in gravitational potential energy of an object is given by the formula:
$\Delta U_g = mgh$
where $\Delta U_g$ is the change in gravitational potential energy, $m$ is the mass of the object, $g$ is the acceleration due to gravity, and $h$ is the vertical height through which the object moves.
In this case, we are given the weight of the object, which is the force due to gravity acting on the object. The weight is related to the mass of the object by the formula:
$F_g = mg$
where $F_g$ is the weight of the object.
Rearranging this formula gives:
$m = \frac{F_g}{g}$
Substituting this expression for $m$ into the formula for $\Delta U_g$, we get:
$\Delta U_g = \frac{F_g}{g}gh = F_gh$
where $F_g$ is the weight of the object, $g$ is the acceleration due to gravity, and $h$ is the vertical height through which the object moves.
Substituting the given values, we get:
$\Delta U_g = (6.10 \times 10^2 \mathrm{~N})(9.81 \mathrm{~m} \mathrm{~s}^{-2})(8.0 \mathrm{~m}) \approx 4.88 \times 10^3 \mathrm{~J}$
Therefore, the correct answer is (C) $4.88 \mathrm{~kJ}$.
Rounding off the answer to two significant figures gives:
$\Delta U_g \approx 4.9 \mathrm{~kJ}$
Therefore, the answer is (B) $4.9 \mathrm{~kJ}$.
