Question
Topic: Uncertainties and errors
Given: A student measures the radius $R$ of a circular plate to determine its area. The absolute uncertainty in $R$ is $\Delta R$.
Calculate: the fractional uncertainty in the area of the plate?
A. $\frac{2 \Delta R}{R}$
B. $\left(\frac{\Delta R}{R}\right)^2$
C. $\frac{2 \pi \Delta R}{R}$
D. $\pi\left(\frac{\Delta R}{R}\right)^2$
▶️Answer/Explanation
Ans:A
Solution:
The area of a circle is given by $A = \pi R^2$. We can use the rules of error propagation to determine the fractional uncertainty in the area of the plate.
First, we can find the absolute uncertainty in the area of the plate as follows:
$$
\Delta A = \left|\frac{\partial A}{\partial R}\right|\Delta R = 2\pi R\Delta R
$$
where $\left|\frac{\partial A}{\partial R}\right|$ is the absolute value of the derivative of $A$ with respect to $R$. We can then find the fractional uncertainty in the area of the plate by dividing $\Delta A$ by the nominal value of $A$:
$$
\frac{\Delta A}{A} = \frac{2\pi R\Delta R}{\pi R^2} = \frac{2\Delta R}{R}
$$
Therefore, the answer is (A) $\frac{2\Delta R}{R}$.
Question
Topic: Unit
Discuss: What is the unit of electrical potential difference expressed in fundamental SI units?
A. $\mathrm{kgms}^{-1} \mathrm{C}^{-1}$
B. $\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-2} \mathrm{C}^{-1}$
C. $\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-3} \mathrm{~A}^{-1}$
D. $\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-1} \mathrm{~A}$
▶️Answer/Explanation
Ans:C
Solution:
The unit of electrical potential difference is volts, which is defined as the amount of potential energy required to move a unit of electric charge between two points in an electric field. In the SI system, the fundamental units of electric potential difference can be expressed as:
– kilogram (kg) for mass
– meter (m) for length
– second (s) for time
– ampere (A) for electric current
Therefore, we need to combine these units to express the unit of electrical potential difference. Using dimensional analysis, we can determine that the correct answer is:
C. $\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-3} \mathrm{~A}^{-1}$
This can be seen by breaking down the definition of the volt in terms of SI base units:
$1 V = 1 J/C$
where J is the unit of energy (joule) and C is the unit of electric charge (coulomb). The unit of joule can be expressed in terms of SI base units as:
$1 J = 1 kg m^2 s^-2$
Substituting this into the definition of the volt gives:
$1 V = 1 J/C = (1 kg m^2 s^-2) / (1 C) = 1 kg m^2 s^-3 A^-1$
Therefore, the unit of electrical potential difference expressed in fundamental SI units is $\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-3} \mathrm{~A}^{-1}$.
Question
Topic: Motion
Given: The graph shows the variation of velocity of a body with time along a straight line.
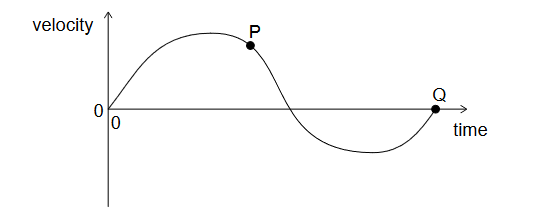
Discuss: What is correct for this graph?
A. The maximum acceleration is at $P$.
B. The average acceleration of the body is given by the area enclosed by the graph and time axis.
C. The maximum displacement is at $\mathrm{Q}$.
D. The total displacement of the body is given by the area enclosed by the graph and time axis.
▶️Answer/Explanation
Ans:D
Solution:
Question
Topic: Vector
Given: Two forces of magnitude $12 \mathrm{~N}$ and $24 \mathrm{~N}$ act at the same point.
Discuss: Which force cannot be the resultant of these forces?
A. $10 \mathrm{~N}$
B. $16 \mathrm{~N}$
C. $19 \mathrm{~N}$
D. $36 \mathrm{~N}$
▶️Answer/Explanation
Ans:A
Solution:
To find the force that cannot be the resultant of two forces of $12\mathrm{~N}$ and $24\mathrm{~N}$, we can use the triangle inequality. According to the triangle inequality, for any triangle with sides $a$, $b$, and $c$, the sum of the lengths of any two sides must be greater than the length of the third side. In this case, the two forces of $12\mathrm{~N}$ and $24\mathrm{~N}$ can be thought of as the two sides of a triangle, and the force we are looking for is the third side (resultant) that cannot be formed by adding the other two sides.
Therefore, we need to check which of the given forces satisfies the triangle inequality with $12\mathrm{~N}$ and $24\mathrm{~N}$. If a force satisfies the triangle inequality, it can be the resultant force of $12\mathrm{~N}$ and $24\mathrm{~N}$. If a force does not satisfy the triangle inequality, it cannot be the resultant force.
we can use the triangle inequality to determine which force cannot be the resultant of the two given forces of $12\mathrm{~N}$ and $24\mathrm{~N}$. The triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side. In this case, we can think of the two forces as the sides of a triangle, and the resultant force as the third side.
The maximum possible resultant force is the sum of the two forces, which is $12\mathrm{~N} + 24\mathrm{~N} = 36\mathrm{~N}$. Therefore, any force greater than $36\mathrm{~N}$ cannot be the resultant force of the two given forces.
The minimum possible resultant force is the absolute value of the difference between the two forces, which is $|12\mathrm{~N} – 24\mathrm{~N}| = 12\mathrm{~N}$. Therefore, any force less than $12\mathrm{~N}$ cannot be the resultant force of the two given forces.
Option (A) is less than the minimum possible resultant force of $12\mathrm{~N}$, and therefore cannot be the resultant force of the two given forces. So the correct answer is $\boxed{\mathrm{(A)}~10\mathrm{~N}}$.
Question
Topic: Work, energy and power
Given: An object has a weight of $6.10 \times 10^2 \mathrm{~N}$.
Calculate: the change in gravitational potential energy of the object when it moves through $8.0 \mathrm{~m}$ vertically?
A. $5 \mathrm{~kJ}$
B. $4.9 \mathrm{~kJ}$
C. $4.88 \mathrm{~kJ}$
D. $4.880 \mathrm{~kJ}$
▶️Answer/Explanation
Ans:B
Solution:
The change in gravitational potential energy of an object is given by the formula:
$\Delta U_g = mgh$
where $\Delta U_g$ is the change in gravitational potential energy, $m$ is the mass of the object, $g$ is the acceleration due to gravity, and $h$ is the vertical height through which the object moves.
In this case, we are given the weight of the object, which is the force due to gravity acting on the object. The weight is related to the mass of the object by the formula:
$F_g = mg$
where $F_g$ is the weight of the object.
Rearranging this formula gives:
$m = \frac{F_g}{g}$
Substituting this expression for $m$ into the formula for $\Delta U_g$, we get:
$\Delta U_g = \frac{F_g}{g}gh = F_gh$
where $F_g$ is the weight of the object, $g$ is the acceleration due to gravity, and $h$ is the vertical height through which the object moves.
Substituting the given values, we get:
$\Delta U_g = (6.10 \times 10^2 \mathrm{~N})(9.81 \mathrm{~m} \mathrm{~s}^{-2})(8.0 \mathrm{~m}) \approx 4.88 \times 10^3 \mathrm{~J}$
Therefore, the correct answer is (C) $4.88 \mathrm{~kJ}$.
Rounding off the answer to two significant figures gives:
$\Delta U_g \approx 4.9 \mathrm{~kJ}$
Therefore, the answer is (B) $4.9 \mathrm{~kJ}$.
