Question.1[(a) (i)].2019-May-Physics_paper_2__TZ2_SL
Topic: Forces
Given: A student strikes a tennis ball that is initially at rest so that it leaves the racquet at a speed of $64 \mathrm{~m} \mathrm{~s}^{-1}$. The ball has a mass of $0.058 \mathrm{~kg}$ and the contact between the ball and the racquet lasts for $25 \mathrm{~ms}$.
Calculate: the average force exerted by the racquet on the ball.
▶️Answer/Explanation
Solution:
To calculate the average force exerted by the racquet on the ball, we can use the impulse-momentum theorem, which relates the impulse applied to an object to the change in its momentum. The impulse is the product of the force and the time during which it acts:
$$
\text{Impulse} = \text{Force} \times \text{Time}
$$
The momentum of the ball before it is struck is zero, since it is at rest. After it is struck, its momentum is:
$$
p = mv = (0.058~\mathrm{kg})(64~\mathrm{m/s}) = 3.712~\mathrm{kg\cdot m/s}
$$
The change in momentum is therefore:
$$
\Delta p = p – 0 = 3.712~\mathrm{kg\cdot m/s}
$$
The time during which the force acts is given as $t=25~\mathrm{ms}=0.025~\mathrm{s}$.
Therefore, the average force exerted by the racquet on the ball is:
$$
\text{Force} = \frac{\text{Impulse}}{\text{Time}} = \frac{\Delta p}{t} = \frac{3.712~\mathrm{kg\cdot m/s}}{0.025~\mathrm{s}} = 148.48~\mathrm{N}
$$
So the average force exerted by the racquet on the ball is $148.48~\mathrm{N}$.
Question.1[(a) (ii)].2019-May-Physics_paper_2__TZ2_SL
Topic:
Calculate: the average power delivered to the ball during the impact.
▶️Answer/Explanation
Solution:
Using the formula for kinetic energy and the definition of power. Plugging in the given values, we get:
$$
E_K = \frac{1}{2}mv^2 = \frac{1}{2}(0.058~\mathrm{kg})(64~\mathrm{m/s})^2 = 118.144~\mathrm{J}
$$
The time during which this energy is transferred is the same as the contact time, which is given as $t=25~\mathrm{ms}=0.025~\mathrm{s}$. Therefore, the average power delivered to the ball during the impact is:
$$
P = \frac{E_K}{t} = \frac{118.144~\mathrm{J}}{0.025~\mathrm{s}} = 4725.76~\mathrm{W} \approx 4.8~\mathrm{kW}
$$
So the average power delivered to the ball during the impact is approximately $4.8~\mathrm{kW}$. This result is consistent with the answer obtained using the impulse-momentum theorem in the previous part of the question.
Question.1[(b) (i)].2019-May-Physics_paper_2__TZ2_SL
Topic:
Given: The student strikes the tennis ball at point $\mathrm{P}$. The tennis ball is initially directed at an angle of $7.00^{\circ}$ to the horizontal.
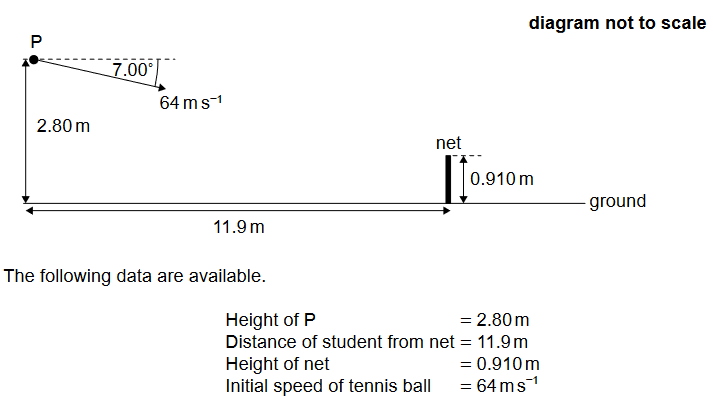
Calculate: the time it takes the tennis ball to reach the net.
▶️Answer/Explanation
Solution:
Constant speed motion to the right at $64 \cos 7^{\circ} \mathrm{m} / \mathrm{s} . \mathrm{d}=11.9 \mathrm{~m}$
$$
\begin{aligned}
& v=\frac{d}{t}=>t=\frac{d}{v} \\
& t=\frac{11.9}{64 \cos 7^{\circ}} \\
& t=0.187 \mathrm{~s}
\end{aligned}
$$
Question.1[(b) (ii)].2019-May-Physics_paper_2__TZ2_SL
Topic:
Show: that the tennis ball passes over the net.
▶️Answer/Explanation
Solution:
Actually, what is the height when ball passes the net.
Lets choose the positive direction upwards: $x=2.80+S$
$\mathrm{T}=0.187 \mathrm{~s}, \mathrm{u}=-64 \sin 7^0=-7.80, \mathrm{a}=-9.81$
Constant acceleration downwards:
$2.1 \mathrm{~s}=u \mathrm{ut}+\frac{1}{2} \mathrm{at}^2$
$S=-7.80 \times 0.187+0.5 \times(-0.981)(0.187)^2$
$\mathrm{S}=-1.63 \mathrm{~m}$
$X=2.80+S$
$X=2.80-1.63$
$X=1.17 \mathrm{~m} \approx 1.2 \mathrm{~m}$ so the height so passes above net $(0.910 \mathrm{~m})$.
Question.1[(b) (iii)].2019-May-Physics_paper_2__TZ2_SL
Topic:
Calculate: the speed of the tennis ball as it strikes the ground.
▶️Answer/Explanation
Solution:
Conservation of energy:
$$
\begin{aligned}
& \triangle K E=\triangle G P E \\
& 1 / 2 m v^2-1 / 2 m u^2=m g H \\
& 1 / 2 m v^2=m g H+1 / 2 \mathrm{mu}^2 \\
& 1 / 2 m v^2=m\left(9.81 \times 2.80+0.5 \times 64^2\right) \\
& 1 / 2 v^2=9.81 \times 2.80+0.5 \times 64^2 \\
& 1 / 2 v^2=2075 \\
& V=\sqrt{2 \times 2075}=64.4 \mathrm{~m} / \mathrm{s}
\end{aligned}
$$
