Question
Topic: Measurements
Discuss: quantity has the fundamental SI units of $\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2} ?$
A. Energy
B. Force
C. Momentum
D. Pressure
▶️Answer/Explanation
Ans:D
Solution:
The quantity that has the fundamental SI units of $\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2}$ is pressure.
Therefore, the answer is D. Pressure.
Pressure is defined as force per unit area and its SI unit is Pascal (Pa). In terms of fundamental SI units, 1 Pa can be expressed as $\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2}$, which matches the given units.
Question
Topic: Vector
An object is held in equilibrium by three forces of magnitude $F, G$ and $H$ that act at a point in the same plane.
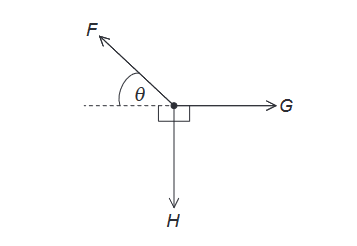
Three equations for these forces are
- $F \cos \theta=G$
- $F=G \cos \theta+H \sin \theta$
- $F=G+H$
Which equations are correct?
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
▶️Answer/Explanation
Ans: A
Solution:
To determine which equations are correct, we can analyze them one by one.
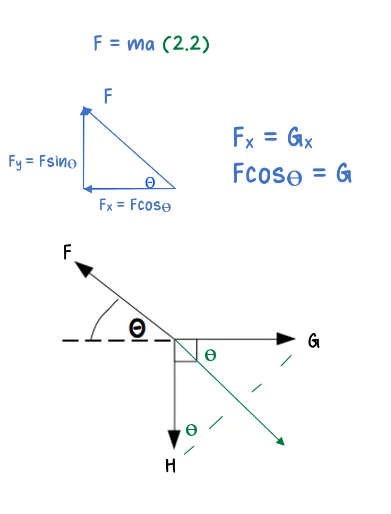
Equation I states that $F \cos \theta=G$. This equation is correct as it describes the horizontal component of the force $F$ being equal to the force $G$ acting horizontally.
Equation II states that $F=G \cos \theta+H \sin \theta$. This equation is also correct as it describes net force is zero if we break component of $G$ and $H$ along the line in which $F$ is acting we will get the result.
Equation III is incorrect because it does not account for the direction of the forces. Without specifying the direction of the forces, it is impossible to determine the magnitude of the resultant force. So, we can conclude that equations I and II are correct, but equation III is incorrect. Therefore, the answer is A.
Question
Topic: Forces
Given: Two forces act along a straight line on an object that is initially at rest. One force is constant; the second force is in the opposite direction and proportional to the velocity of the object.

Discuss: correct about the motion of the object?
A. The acceleration increases from zero to a maximum.
B. The acceleration increases from zero to a maximum and then decreases.
C. The velocity increases from zero to a maximum.
D. The velocity increases from zero to a maximum and then decreases.
▶️Answer/Explanation
Ans:C
Solution:
Since one force is constant and the other force is proportional to the velocity and in the opposite direction, the net force acting on the object decreases as the object’s velocity increases. At some point, the opposing force becomes equal in magnitude to the constant force, resulting in zero net force and a constant velocity.
Initially, when the object is at rest, the net force is equal to the constant force. Therefore, the object accelerates in the direction of the constant force. As the velocity increases, the opposing force also increases proportionally, slowing down the acceleration. Eventually, the opposing force becomes equal to the constant force, and the net force acting on the object becomes zero. At this point, the object moves with a constant velocity, which is the maximum velocity attained during the motion. Therefore, the correct option is C. The velocity increases from zero to a maximum.
Question
Topic: Momentum and impulse
Given: The variation with time $t$ of the acceleration a of an object is shown.
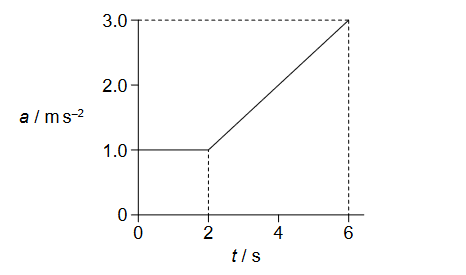
Calculate: the change in velocity of the object from $t=0$ to $t=6 \mathrm{~s}$ ?
A. $6 \mathrm{~ms}^{-1}$
B. $8 \mathrm{~ms}^{-1}$
C. $10 \mathrm{~m} \mathrm{~s}^{-1}$
D. $14 \mathrm{~m} \mathrm{~s}^{-1}$
▶️Answer/Explanation
Ans:C
Solution:
The change in velocity of the object from $t=0$ to $t=6 \mathrm{~s}$ can be determined by finding the area under the acceleration-time graph between these two times. This area represents the change in velocity of the object during this time interval, according to the kinematic equation:
$\Delta v = \int_{t_1}^{t_2} a(t) dt$
Using the graph, we can see that the acceleration of the object is constant at $1 \mathrm{~ms}^{-2}$ between $t=0$ and $t=2 \mathrm{~s}$. Therefore, we can calculate the change in velocity during this time interval as:
$\Delta v_1 = a_1 \Delta t = 1 \mathrm{~ms}^{-2} \times 2 \mathrm{~s} = 2 \mathrm{~ms}^{-1}$
Between $t=2 \mathrm{~s}$ and $t=6 \mathrm{~s}$, the acceleration of the object varies linearly from $1 \mathrm{~ms}^{-2}$ to $3 \mathrm{~ms}^{-2}$. Therefore, we can calculate the change in velocity during this time interval as the area of a trapezium:
$\Delta v_2 = \frac{1}{2} (a_1 + a_2) \Delta t = \frac{1}{2} (1 \mathrm{~ms}^{-2} + 3 \mathrm{~ms}^{-2}) \times 4 \mathrm{~s} = 8 \mathrm{~ms}^{-1}$
The total change in velocity of the object from $t=0$ to $t=6 \mathrm{~s}$ is therefore:
$\Delta v = \Delta v_1 + \Delta v_2 = 2 \mathrm{~ms}^{-1} + 8 \mathrm{~ms}^{-1} = 10 \mathrm{~ms}^{-1}$
Therefore, the correct answer is the option C.
Question
Topic: Forces
Given: A climber of mass $m$ slides down a vertical rope with an average acceleration $a$.
Calculate: the average frictional force exerted by the rope on the climber?
A. $m g$
B. $m(g+a)$
C. $m(g-a)$
D. $ma$
▶️Answer/Explanation
Ans:C
Solution:
Since the climber is sliding down the rope, the frictional force is opposing the motion and acting upwards. The net force acting on the climber is the difference between the gravitational force and the frictional force, which is given by:
$$
F_{net} = m(g) – f = ma
$$
where $f$ is the frictional force and $g$ is the acceleration due to gravity. Solving for $f$, we get:
$$
f = m(g – a)
$$
So the correct answer is (C) $m(g – a)$.
