Question-1 (a) :2021-nov-Chemistry_paper_2__TZ0_HL
Topic:
Given: A $4.406 \mathrm{~g}$ sample of a compound containing only $\mathrm{C}, \mathrm{H}$ and $\mathrm{O}$ was burnt in excess oxygen. $8.802 \mathrm{~g}$ of $\mathrm{CO}_2$ and $3.604 \mathrm{~g}$ of $\mathrm{H}_2 \mathrm{O}$ were produced.
Calculate: the empirical formula of the compound using section 6 of the data booklet.
Answer/Explanation
Solution:
We can calculate the empirical formula of the compound by using the masses of carbon, hydrogen, and oxygen in the sample. To do this, we first need to calculate the number of moles of carbon and hydrogen in the sample using the masses of $\mathrm{CO_2}$ and $\mathrm{H_2O}$ produced, as we did earlier:
$$n_{\mathrm{C}} = \frac{m_{\mathrm{CO_2}}}{M_{\mathrm{CO_2}}} = \frac{8.802~\mathrm{g}}{44.01~\mathrm{g/mol}} \approx 0.1998~\mathrm{mol}$$
$$n_{\mathrm{H}} = 2\times\frac{m_{\mathrm{H_2O}}}{M_{\mathrm{H_2O}}} = 2\times\frac{3.604~\mathrm{g}}{18.015~\mathrm{g/mol}} = 0.3998~\mathrm{mol}$$
Next, we can calculate the masses of carbon and hydrogen in the sample using their respective molar masses:
$$m_{\mathrm{C}} = n_{\mathrm{C}}\times M_{\mathrm{C}} = 0.1998~\mathrm{mol} \times 12.01~\mathrm{g/mol} = 2.401~\mathrm{g}$$
$$m_{\mathrm{H}} = n_{\mathrm{H}}\times M_{\mathrm{H}} = 0.3998~\mathrm{mol} \times 1.008~\mathrm{g/mol} = 0.402~\mathrm{g}$$
Finally, we can calculate the mass of oxygen in the sample by subtracting the masses of carbon and hydrogen from the total mass of the sample:
$$m_{\mathrm{O}} = m_{\mathrm{sample}} – m_{\mathrm{C}} – m_{\mathrm{H}} = 4.406~\mathrm{g} – 2.401~\mathrm{g} – 0.402~\mathrm{g} = 1.603~\mathrm{g}$$
Now we have the masses of carbon, hydrogen, and oxygen in the sample, and we can calculate the empirical formula of the compound by dividing each mass by its respective molar mass and then dividing by the smallest resulting value:
$$\begin{array}{c|ccc} \mathrm{Element} & \mathrm{C} & \mathrm{H} & \mathrm{O} \\ \hline \mathrm{Mass~(g)} & 2.401 & 0.402 & 1.603 \\ \mathrm{Molar~mass~(g/mol)} & 12.01 & 1.008 & 16.00 \\ \mathrm{Number~of~moles} & 0.1998 & 0.3998 & 0.1002 \\ \mathrm{Mole~ratio}\approx & 2 & 4 & 1 \end{array}$$
So the empirical formula of the compound is also $\mathrm{C_2H_4O}$.
Question-1 (b) :2021-nov-Chemistry_paper_2__TZ0_HL
Topic:
Determine the molecular formula of this compound if its molar mass is $88.12 \mathrm{~g} \mathrm{~mol}^{-1}$. If you did not obtain an answer in (a) use CS, but this is not the correct answer.
Answer/Explanation
Solution:
Since the empirical formula of the compound is $\mathrm{C}_2\mathrm{H}_4\mathrm{O}$ with a molar mass of $88.12~\mathrm{g~mol^{-1}}$, we can calculate the empirical formula mass as follows:
$\mathrm{C}_2\mathrm{H}_4\mathrm{O} = (2 \times 12.01) + (4 \times 1.01) + (16.00) = 44.06~\mathrm{g~mol^{-1}}$
To determine the molecular formula of the compound, we need to know how many times the empirical formula must be multiplied to get the molar mass of the actual compound. We can find this factor by dividing the molar mass of the actual compound by the empirical formula mass:
$\text{Factor} = \dfrac{88.12~\mathrm{g~mol^{-1}}}{44.06~\mathrm{g~mol^{-1}}} = 2$
This means that the molecular formula of the compound is twice the empirical formula, so we need to multiply the subscripts in the empirical formula by 2 to get the molecular formula:
$\mathrm{C}_2\mathrm{H}_4\mathrm{O} \times 2 = \mathrm{C}_4\mathrm{H}_8\mathrm{O}_2$
Therefore, the molecular formula of the compound is $\mathrm{C}_4\mathrm{H}_8\mathrm{O}_2$.
Question-1 (c) :2021-nov-Chemistry_paper_2__TZ0_HL
Topic:
Given: The following spectrums show the Infrared spectra of propan-1-ol, propanal and propanoic acid.
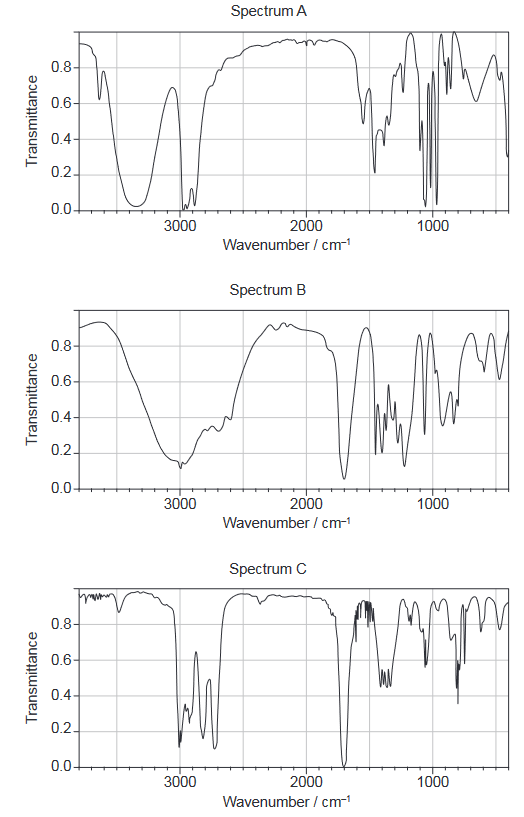
Discuss: each compound from the spectra given, use absorptions from the range of $1700 \mathrm{~cm}^{-1}$ to $3500 \mathrm{~cm}^{-1}$. Explain the reason for your choice, referring to section 26 of the data booklet.

Answer/Explanation
Solution:

Question-1 (d) :2021-nov-Chemistry_paper_2__TZ0_HL
Topic:
Discuss: the number of ${ }^1 \mathrm{HNMR}$ signals, and splitting pattern of the $-\mathrm{CH}_3$ seen for propanone $\left(\mathrm{CH}_3 \mathrm{COCH}_3\right)$ and propanal $\left(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHO}\right)$.
Answer/Explanation
Solution:
Propanone ($\mathrm{CH_3COCH_3}$) has two different types of protons: the methyl group ($-\mathrm{CH}_3$) and the methylene group ($-\mathrm{CH}_2-$), which are both equivalent. Therefore, propanone would have one ${}^1\mathrm{H}$ NMR signal, which would appear as a singlet.
Propanal ($\mathrm{CH_3CH_2CHO}$) has three different types of protons: the methyl group ($-\mathrm{CH}_3$) which would appear as a singlet, the methylene group ($-\mathrm{CH}_2-$) which would appear as a quartet, and the aldehyde proton ($-\mathrm{CHO}$) which would appear as a doublet. Therefore, propanal would have three ${}^1\mathrm{H}$ NMR signals.
Question-1 (e) :2021-nov-Chemistry_paper_2__TZ0_HL
Topic:
Discuss: the fragment that is responsible for a $\mathrm{m} / \mathrm{z}$ of 31 in the mass spectrum of propan-1-ol. Use section 28 of the data booklet.
Answer/Explanation
Solution:
The $\mathrm{m}/\mathrm{z}$ of 31 corresponds to the fragment $\mathrm{CH_3O^+}$ in the mass spectrum of propan-1-ol. This fragment is formed when the molecular ion ($\mathrm{M}$) of propan-1-ol ($\mathrm{C_3H_8O}$) undergoes fragmentation in the mass spectrometer, losing a neutral $\mathrm{CH_3OH}$ molecule.
The fragmentation of the molecular ion of propan-1-ol can be represented as follows:
$\mathrm{M} \rightarrow \mathrm{CH_3O^+} + \mathrm{C_2H_5OH}$
The $\mathrm{CH_3O^+}$ fragment has a mass of 31 $\mathrm{u}$, which corresponds to the $\mathrm{m}/\mathrm{z}$ value observed in the mass spectrum.
