Q.1.2021-Nov-Physics_paper_1__TZ0_SL
Topic: Vectors and scalars
Discuss: Which is a vector quantity?
A. Acceleration
B. Energy
C. Pressure
D. Speed
Answer/Explanation
Solution:
Acceleration is a vector quantity.
$\colorbox{yellow}{Correct Option-A}$
Q.2.2021-Nov-Physics_paper_1__TZ0_SL
Topic: Uncertainties and errors
Given: A ball of mass (50 ± 1)g is moving with a speed of (25 ± 1)ms-1.
Calculate: What is the fractional uncertainty in the momentum of the ball?
A. $0.02$
B. $0.04$
C.$ 0.06$
D.$ 0.08$
Answer/Explanation
Solution
$\begin{aligned} & p=m v \\ & \frac{\Delta p}{p}=\frac{\Delta m}{m}+\frac{\Delta v}{v}=\frac{1}{50}+\frac{1}{25} \\ & =\frac{3}{50}\Rightarrow 0.06 \\ & \end{aligned}$
$\colorbox{yellow}{Correct Option-C}$
Q.3.2021-Nov-Physics_paper_1__TZ0_SL
Topic: Motion
Given: The graph shows the variation with time t of the velocity of an object.
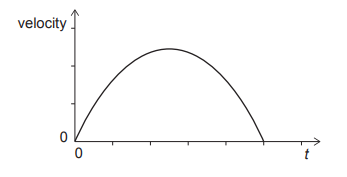
Calculation: What is the variation with time t of the acceleration of the object?
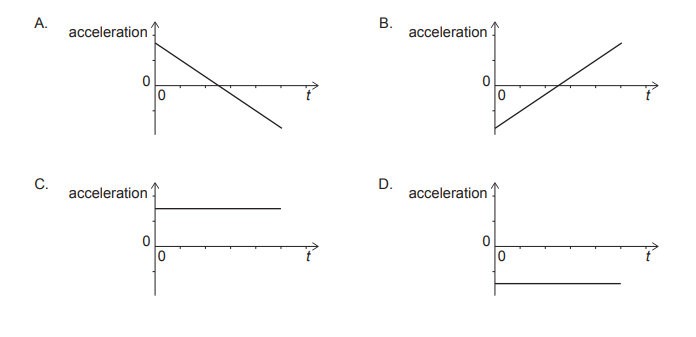
Answer/Explanation
Solution:
$\begin{aligned} & v \propto-t^2 \\ & \frac{d v}{d t} \propto-2 t \\ & a \propto-2 t\end{aligned}$
$\colorbox{yellow}{Correct Option-A}$
Q.4.2021-Nov-Physics_paper_1__TZ0_SL
Topic: Motion
Given: A ball is thrown vertically downwards with an initial speed of $4.0 \mathrm{~ms}^{-1}$. The ball hits the ground with a speed of $16 \mathrm{~ms}^{-1}$. Air resistance is negligible.
Calculate: What is the time of fall and what is the distance travelled by the ball?
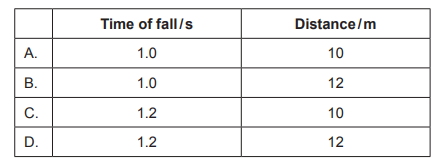
Answer/Explanation
Solution:
We can use the equations of motion to solve this problem. Since the ball is thrown vertically downwards, we can take the positive direction as downwards.
Initial speed, $u = 4.0~\mathrm{ms^{-1}}$
Final speed, $v = 16~\mathrm{ms^{-1}}$
Acceleration, $a = g = 10~\mathrm{ms^{-2}}$ (acceleration due to gravity)
We can use the equation $v^2 = u^2 + 2as$ to find the distance travelled by the ball:
$v^2 = u^2 + 2as$
$16^2 = 4^2 + 2 \times 10 \times s$
$s = \frac{16^2 – 4^2}{2 \times 10} = 12~\mathrm{m}$
So, the ball travels a distance of $\boxed{12~\mathrm{m}}$
We can use the equation $v = u + at$ to find the time of fall:
$v = u + at$
$16 = 4 + 10t$
$t = \frac{16 – 4}{10} = 1.2~\mathrm{s}$
So, the time of fall is $\boxed{1.2~\mathrm{s}}$
