2023-May-Chemistry_paper_1__TZ2_SL
Topic: Reacting masses and volumes
Discuss: Correct equation for the electrolysis of molten sodium chloride?
A. \(2NaCl(l) → 2Na(l) + Cl_2 (g)\)
B. \(2NaCl(s) → 2Na(s) + Cl_2 (g)\)
C. \(2NaCl(l) → 2Na(s) + Cl_2 (g)\)
D. \(2NaCl(aq) → 2Na(s) + Cl_2 (g)\)
▶️Answer/Explanation
Markscheme: A
The electrolysis of molten sodium chloride (\(NaCl\)) involves the breaking down of the compound into its constituent elements, sodium (\(Na\)) and chlorine (\(Cl_2\)), through the application of an electric current.
The balanced chemical equation for the electrolysis of molten sodium chloride is:
\[ 2NaCl(l) \rightarrow 2Na(l) + Cl_2(g) \]
This process takes place in a molten state, meaning that the sodium chloride is melted to form a liquid. The electric current is passed through the molten salt, leading to the reduction of sodium ions (\(Na^+\)) to form sodium metal (\(Na\)) at the cathode and the oxidation of chloride ions (\(Cl^-\)) to form chlorine gas (\(Cl_2\)) at the anode.
2023-May-Chemistry_paper_1__TZ2_SL
Topic: Mole concepts
Calculate: Mass of one molecule of \(C_{60}\) ?
A. \(1.0 \times 10^{-22}\)
B. \(2.0 \times 10^{-23}\) g
C. \(8.3 \times 10^{-24}\) g
D. \(1.2 \times 10^{-21}\) g
▶️Answer/Explanation
Markscheme: D
The molecular mass of a substance in grams is equal to its molar mass, which is numerically equal to the molecular weight (mass) of one mole of the substance.
The molecular formula for \(C_{60}\) (Buckminsterfullerene, also known as a buckyball) represents a molecule with 60 carbon atoms. The molar mass of \(C_{60}\) can be calculated by adding the atomic masses of 60 carbon atoms.
The atomic mass of carbon (\(C\)) is approximately 12.01 g/mol.
\[ \text{Molar mass of } C_{60} = 60 \times \text{Atomic mass of } C \]
\[ \text{Molar mass of } C_{60} = 60 \times 12.01 \, \text{g/mol} \]
\[ \text{Molar mass of } C_{60} = 720.6 \, \text{g/mol} \]
Now, to find the mass of one molecule of \(C_{60}\), we need to divide this molar mass by Avogadro’s number (\(N_A\)).
\[ \text{Mass of one molecule of } C_{60} = \frac{\text{Molar mass}}{N_A} \]
\[ \text{Mass of one molecule of } C_{60} = \frac{720.6 \, \text{g/mol}}{6.0 \times 10^{23} \, \text{mol}^{-1}} \]
\[ \text{Mass of one molecule of } C_{60} \approx 1.2 \times 10^{-21} \, \text{g} \]
2023-May-Chemistry_paper_1__TZ2_SL
Topic: Stoichiometric relationships
Given: 20\(cm^3\) of gas A reacts with 20\(cm^3\) of gas B to produce 10\(cm^3\) of gas \(A_xB_y\) and 10\(cm_3\) of excess gas A.
Calculate: Correct values for subscripts x and y in the empirical formula of the product \(A_xB_y\) (g)?
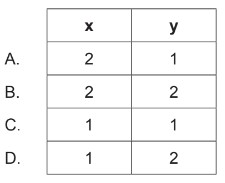
▶️Answer/Explanation
Markscheme: D
Let’s analyze the information provided:
1. \(20 \mathrm{~cm}^3\) of gas A reacts with \(20 \mathrm{~cm}^3\) of gas B.
2. The reaction produces \(10 \mathrm{~cm}^3\) of gas \(A_xB_y\) and \(10 \mathrm{~cm}^3\) of excess gas A.
From this information, we can deduce the following:
The initial moles of A and B are equal since the volumes are the same.
The reaction consumes all of B, as there is no excess of B mentioned.
\(10 \mathrm{~cm}^3\) of excess gas A remains unreacted.
Given that excess gas A is \(10 \mathrm{~cm}^3\), and \(10 \mathrm{~cm}^3\) of gas \(A_xB_y\) is produced, it implies that \(A_xB_y\) is formed by the combination of \(A\) and \(B\), and the remaining \(10 \mathrm{~cm}^3\) of A is in excess.
Since \(A_xB_y\) is formed from 20 \(\mathrm{cm}^3\) of A and 20 \(\mathrm{cm}^3\) of B, and the excess A is 10 \(\mathrm{cm}^3\), it suggests that the composition of \(A_xB_y\) is 1 part A and 2 parts B.
Therefore, the correct values for subscripts \(x\) and \(y\) in the empirical formula of the product \(A_xB_y\) are: \[ A_1B_2 \]
2023-May-Chemistry_paper_1__TZ2_SL
Topic: Gas Laws
Given: The volume V for a fixed mass of an ideal gas was measured at constant temperature at different pressures p.
Calculate:Graph shows the correct relationship between pV against p?
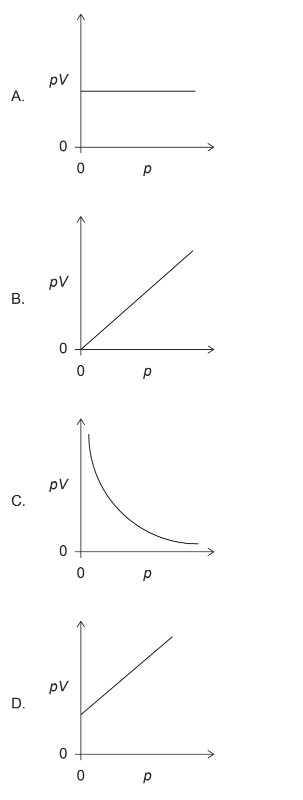
▶️Answer/Explanation
Markscheme: A
For an ideal gas at constant temperature, the relationship between pressure (\(p\)) and volume (\(V\)) is given by Boyle’s Law, which states that the product of pressure and volume is constant:
\[ pV = \text{constant} \]
This implies that \(pV\) is a constant value for an ideal gas at constant temperature.
Therefore, the correct relationship between \(pV\) and \(p\) is a horizontal line on a graph.
2023-May-Chemistry_paper_1__TZ2_SL
Topic:Periodic Table
Calculate: Correct ground state electron orbital configuration for \(2s^22p^2\)?
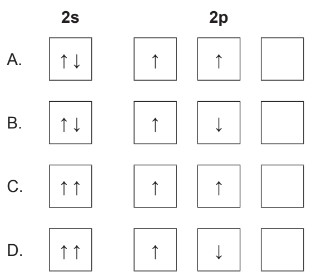
▶️Answer/Explanation
Markscheme: A
According to the Pauli Exclusion Principle, no two electrons in an atom can have the same set of four quantum numbers. This means that electrons in the same orbital must have opposite spins. Each orbital can accommodate a maximum of 2 electrons with opposite spins.
\(2 s^2\) represents the electron configuration for the 2s subshell, which can hold up to 2 electrons with opposite spin.
In the case of the \(2 p\) subshell, there are three individual orbitals labeled \(2 p_x, 2 p_y\), and \(2 p_z\). Each of these orbitals can hold up to 2 electrons with opposite spins. Two electrons are in the \(2 \mathrm{p}\) subshell, one in \(2 p_x\) with spin \(\uparrow\) and the other in \(2 p_y\) with spin \(\uparrow\).
To satisfy the Pauli Exclusion Principle, the two electrons in the \(2 p^2\) configuration must have opposite spins and must be placed in different orbitals within the \(2 p\) subshell.
So, the correct distribution is one electron in \(2 p_x\) with spin \(\uparrow\) and the other electron in \(2 p_y\) with spin \(\uparrow\). This ensures that both electrons have unique sets of quantum numbers, complying with the Pauli Exclusion Principle.