Question
Ammonia reacts with oxygen to produce nitrogen (II) oxide and water.
$
\_\mathrm{NH}_3(\mathrm{~g})+\ldots \mathrm{O}_2(\mathrm{~g}) \rightarrow \ldots \mathrm{NO}(\mathrm{g})+\ldots \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$
What is the \(\mathrm{NH}_3: \mathrm{O}_2\) ratio in the balanced equation?
A. \(2: 5\)
B. \(4: 5\)
C. 1:1
D. \(2: 1\)
▶️Answer/Explanation
Ans:B
The balanced equation for the reaction of ammonia with oxygen to produce nitrogen (II) oxide and water is
4\mathrm{NH}_3(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightarrow 4 \mathrm{NO}(\mathrm{g})+6\mathrm{H}_2 \mathrm{O}(\mathrm{l})
$
So, the \(\mathrm{NH}_3: \mathrm{O}_2\) ratio in the balanced equation is \(4:5\). Therefore, the correct answer is B. \(4: 5\).
Question
Metal \(\mathrm{M}\) reacts with \(16.0 \mathrm{~g}\) of sulfur to produce \(26.0 \mathrm{~g}\) of the compound \(\mathrm{MS}_2\). What is the relative atomic mass of \(\mathrm{M}\) ?
A. 5
B. 10
C. 20
D. 40
▶️Answer/Explanation
Ans:D
1. Calculate the number of moles of sulfur \((S\) ):
Number of moles of \(S=\frac{16.0 \mathrm{~g}}{32.06 \mathrm{~g} / \mathrm{mol}}=0.499\) moles
2. Calculate the number of moles of the compound \(\left(\mathrm{MS}_2\right)\) :
Number of moles of \(\mathrm{MS}_2=\frac{26.0 \mathrm{~g}}{32.06 \mathrm{~g} / \mathrm{mol}}=0.810\) moles
3. Calculate the number of moles of metal \((M)\) :
Since there are 2 moles of sulfur for every mole of metal in the compound, the number of moles of metal \((M)\) is half of the number of moles of the compound.
Number of moles of \(M=\frac{0.810 \text { moles }}{2}=0.405\) moles
4. Find the molar mass of metal \((M)\) :
Molar mass of \(M=\frac{16.0 \mathrm{~g}}{0.405 \text { moles }} \approx 39.5 \mathrm{~g} / \mathrm{mol}\)
Now, we’ve correctly calculated the molar mass of \(M\) to be approximately \(39.5 \mathrm{~g} / \mathrm{mol}\), which is closest to option D. So, the correct answer is D. \(\mathbf{4 0}\).
Question
\(64 \mathrm{~g}\) of methane and \(96 \mathrm{~g}\) of oxygen are reacted according to the equation.
$
\mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$
What would be found in the reaction vessel at completion of the reaction?
A. \(\mathrm{CO}_2(\mathrm{~g})\) and \(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\) only
B. \(\mathrm{O}_2(\mathrm{~g}), \mathrm{CO}_2(\mathrm{~g})\) and \(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\) only
C. \(\mathrm{CH}_4(\mathrm{~g}), \mathrm{CO}_2(\mathrm{~g})\) and \(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\) only
D. \(\mathrm{CH}_4(\mathrm{~g}), \mathrm{O}_2(\mathrm{~g}), \mathrm{CO}_2(\mathrm{~g})\) and \(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)
▶️Answer/Explanation
Ans:C
The molar mass of methane \((\mathrm{CH}_4)\) is approximately 16 g/mol and that of oxygen \((\mathrm{O}_2)\) is approximately 32 g/mol.
Given that we have 64 g of methane, this corresponds to \(64 \mathrm{~g} / 16 \mathrm{~g/mol} = 4\) moles of methane. Similarly, 96 g of oxygen corresponds to \(96 \mathrm{~g} / 32 \mathrm{~g/mol} = 3\) moles of oxygen.
From the balanced chemical equation, we can see that one mole of methane reacts with two moles of oxygen. Therefore, 4 moles of methane would require 8 moles of oxygen for the reaction to go to completion. However, we only have 3 moles of oxygen, which is not enough to react with all the methane.
Therefore, at the completion of the reaction, there will be leftover methane \((\mathrm{CH}_4)\), along with the products of the reaction, carbon dioxide \((\mathrm{CO}_2)\) and water \((\mathrm{H}_2\mathrm{O})\).
So, the correct answer is C.
Question
Gallium \(\left(A_r=69.72\right)\) consists of two stable isotopes, Ga-69 and Ga-71. What is the relative abundance of Ga-71?
A. \(36 \%\)
B. \(40 \%\)
C. \(60 \%\)
D. \(64 \%\)
▶️Answer/Explanation
Ans:A
Atomic mass of \(\mathrm{Ga}-69\left(\mathrm{Ga}_{69}\right)=69\)
Atomic mass of Ga-71 \(\left(\mathrm{Ga}_{71}\right)=71\)
Average atomic mass \(\left(\mathrm{A}_{\text {avg }}\right)=69.72\)
\[
\mathrm{A}_{\mathrm{avg}}=\left(\frac{x}{100} \times \mathrm{A}_{69}\right)+\left(\frac{(100-x)}{100} \times \mathrm{A}_{71}\right)
\]
\[
\begin{aligned}
& 69.72=\left(\frac{x}{100} \times 69\right)+\left(\frac{(100-x)}{100} \times 71\right) \\
& 69.72=0.69 x+0.71(100-x) \\
& 69.72=0.69 x+71-0.71 x \\
& 69.72-71=-0.02 x \\
& -1.28=-0.02 x \\
& x=\frac{-1.28}{-0.02} \\
& x=64
\end{aligned}
\]
Thus, the relative abundance of Ga- 71 is indeed \(100-x=36 \%\), which corresponds to option A.
Question
The first three ionization energies for two elements, \(X\) and \(Y\), are: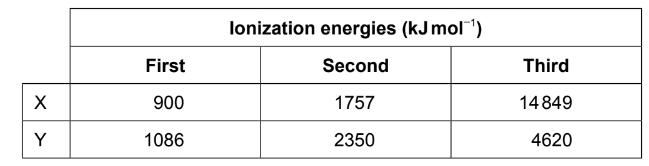
Which pair of elements represent \(X\) and \(Y\), respectively?
A. Lithium and beryllium
B. Lithium and carbon
C. Beryllium and carbon
D. Helium and beryllium
▶️Answer/Explanation
Ans:C
To identify the elements \(X\) and \(Y\), we can analyze their ionization energies.
Lithium (\(Li\)) has atomic number \(3\), and beryllium (\(Be\)) has atomic number \(4\). Carbon (\(C\)) has atomic number \(6\), and helium (\(He\)) has atomic number \(2\).
Let’s compare the ionization energies given for \(X\) and \(Y\) with the known ionization energies for these elements:
- The first ionization energy of \(Li\) is around \(520 \, \text{kJ/mol}\), while the first ionization energy of \(Be\) is around \(900 \, \text{kJ/mol}\). The first ionization energy of \(He\) is around \(524 \, \text{kJ/mol}\). None of these matches \(X\).
- The second ionization energy of \(Li\) is around \(7300 \, \text{kJ/mol}\), while the second ionization energy of \(Be\) is around \(1757 \, \text{kJ/mol}\). The second ionization energy of \(He\) is significantly higher than both, around \(7485 \, \text{kJ/mol}\). None of these matches \(Y\).
- The third ionization energy of \(Li\) is significantly higher than all the values given for \(X\). The third ionization energy of \(Be\) is \(14849 \, \text{kJ/mol}\), which matches \(X\). The third ionization energy of \(He\) is negligible compared to the given values, so it doesn’t match \(X\).
Thus, element \(X\) is beryllium (\(Be\)).
Now, we’re left with only one option for element \(Y\), which is carbon (\(C\)), as its second ionization energy is \(2350 \, \text{kJ/mol}\), matching the value given for \(Y\).
So, the correct pair is:
C. Beryllium and carbon