2023-Nov-Physics_paper_1__TZ0_SL
Topic: Physical Quantity
Given: The resistive force \(F\) that acts on an object moving through a fluid at speed \(v\) is given by \(F=k v\) where \(k\) is a constant.
Calculate: the unit of \(k\) ?
A. \(\mathrm{Ns}^{-1}\)
B. \(\mathrm{Nms}^{-1}\)
C. \(\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-3}\)
D. \(\mathrm{kg} \mathrm{s}^{-1}\)
▶️Answer/Explanation
Ans:D
The resistive force (F) is given by \(F = k \cdot v\), where (F) is the force in Newtons (N), (v) is the velocity in meters per second (m/s), and (k) is a constant.
The unit of (k) can be determined by rearranging the equation to solve for (k):
\(k = \frac{F}{v}\)
Given that the unit of force (F) is Newtons (N) and the unit of velocity (v) is meters per second (m/s), the unit of (k) is Newtons per meter per second \((\mathrm{N/(m/s)})\), which simplifies to \(\mathrm{kg/s}\).
2023-Nov-Physics_paper_1__TZ0_SL
Topic: Forces
Given: A pendulum is displaced by angle \(\theta\) and released from rest.
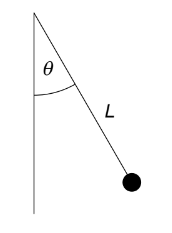
Calculate: the initial acceleration of the pendulum?
A. zero
B. \(g \sin \theta\)
C. \(g \cos \theta\)
D. \(g\)
▶️Answer/Explanation
Ans:B
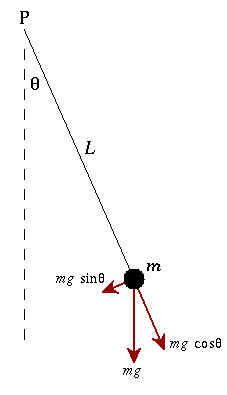
The initial acceleration of the pendulum can be determined by analyzing the forces acting on it when displaced by an angle \(\theta\). The force of gravity will have a component acting along the arc of the pendulum’s swing, which is responsible for the pendulum’s acceleration back towards its equilibrium position.
This component of the gravitational force can be calculated using the formula \(mg \sin \theta\), where (m) is the mass of the pendulum and (g) is the acceleration due to gravity. Since the mass (m) cancels out when calculating acceleration, the initial acceleration (a) of the pendulum is given by:
\[a = g \sin \theta\]
2023-Nov-Physics_paper_1__TZ0_SL
Topic: Forces
Given: Particle \(X\) moves in a circle with a constant speed \(v\). The net force on \(X\) is \(F_X\). Particle \(Y\) moves with a constant velocity, the magnitude of the velocity is \(v\). The net force on \(Y\) is \(F_Y\).
Discuss: Which of the following is correct?
A. \(F_{\mathrm{X}}>F_{\mathrm{Y}}\)
B. \(F_X=F_{\mathrm{Y}} \neq 0\)
C. \(F_{\mathrm{X}}<F_{\mathrm{Y}}\)
D. \(F_X=F_{\mathrm{Y}}=0\)
▶️Answer/Explanation
Ans:A
The correct answer is A. \(F_{\mathrm{X}}>F_{\mathrm{Y}}\).
Here’s why:
Particle (X) is moving in a circle with a constant speed. This is a case of uniform circular motion. Even though the speed is constant, the direction of the velocity is continuously changing (since it’s moving in a circle), which means the particle is accelerating. According to Newton’s second law, a net force is required to cause this acceleration, and this force is directed towards the center of the circle. So, \(F_X\) is not zero.
Particle (Y) is moving with a constant velocity. This means both the speed and the direction of motion are constant. Therefore, there is no acceleration. According to Newton’s first law, if an object is in a state of uniform motion, it will continue to be in that state unless acted upon by an external force. So, in this case, the net force \(F_Y\) is zero.
2023-Nov-Physics_paper_1__TZ0_SL
Topic: Projectile Motion
Given: A projectile is launched with an initial kinetic energy \(E\). The initial horizontal and vertical components of velocity are equal. Air resistance is negligible.
Calculate: kinetic energy of the projectile at the highest point of the motion?
A. zero
B. \(\frac{E}{4}\)
C. \(\frac{E}{2}\)
D. \(E\)
▶️Answer/Explanation
Ans:C
The correct answer is C. \(\frac{E}{2}\).
Here’s why:
At the highest point of the motion, the vertical component of the velocity becomes zero (since it momentarily stops before changing direction), but the horizontal component of the velocity remains unchanged (since there is no air resistance).
Since the initial kinetic energy was equally divided between the vertical and horizontal components of the velocity, and the vertical component of the velocity is now zero, the kinetic energy at the highest point is half of the initial kinetic energy.
2023-Nov-Physics_paper_1__TZ0_SL
Topic: Work, energy and power
Given: An object falls from rest in vacuum. \(R\) is the rate of the change of kinetic energy with time \(t\).
Discuss: How does \(R\) vary with \(t\) ?
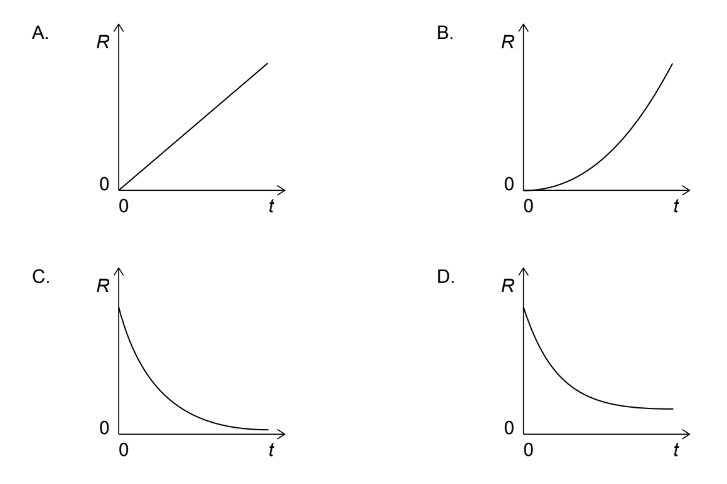
▶️Answer/Explanation
Ans:A
In a vacuum, an object falling from rest is subject only to the force of gravity. The acceleration due to gravity is constant, denoted by (g).
The velocity (v) of the object at time (t) is given by (v = gt), since it starts from rest.
The kinetic energy (K) of the object at time (t) is given by \(K = \frac{1}{2} m v^2 = \frac{1}{2} m g^2 t^2\), where (m) is the mass of the object.
The rate of change of kinetic energy with time (R) is the derivative of (K) with respect to (t), which gives us \(R = m g^2 t\).
So, (R) is directly proportional to (t). As (t) increases, (R) increases linearly. Therefore, the rate of change of kinetic energy with time is not constant, but increases over time at a constant rate.
