2023-Nov-Physics_paper_2__TZ0_SL – All Questions with detailed solution
Question
A space probe of mass \(95 \mathrm{~kg}\) is designed to land on the surface of an asteroid. The gravitational field strength \(g\) of the asteroid at its surface is \(2.7 \times 10^{-3} \mathrm{~m} \mathrm{~s}^{-2}\).
(a) The radius \(r\) of the asteroid is \(230 \mathrm{~km}\). Calculate the mass of the asteroid.[2]
▶️Answer/Explanation
Ans:
To calculate the mass of the asteroid, we can use Newton’s law of universal gravitation, which states:
\[ g = \frac{G \cdot M}{r^2} \]
Where:
\( g \) is the gravitational field strength (\(2.7 \times 10^{-3} \, \text{m/s}^2\))
\( G \) is the gravitational constant (\(6.67430 \times 10^{-11} \, \text{m}^3/\text{kg/s}^2\))
\( M \) is the mass of the asteroid (what we’re trying to find)
\( r \) is the radius of the asteroid (\(230 \, \text{km}\))
\[ M = \frac{g \cdot r^2}{G} \]
\[ M = \frac{(2.7 \times 10^{-3} \, \text{m/s}^2) \cdot (230 \times 10^3 \, \text{m})^2}{6.67430 \times 10^{-11} \, \text{m}^3/\text{kg/s}^2} \]
\[ M = \frac{(2.7 \times 10^{-3}) \cdot (230 \times 10^3)^2}{6.67430 \times 10^{-11}} \, \text{kg} \]
\[ M \approx 2.121 \times 10^{18} \, \text{kg} \]
So, the mass of the asteroid is approximately \(2.121 \times 10^{18} \, \text{kg}\).
Question
(b) The probe is carried to the asteroid on board a spacecraft.
Calculate the weight of the probe when close to the surface of the asteroid. [1]
▶️Answer/Explanation
Ans:
The weight of an object is given by the formula:
\[ \text{Weight} = m \cdot g \]
Where:
\( m \) is the mass of the object (in this case, the mass of the space probe),
\( g \) is the acceleration due to gravity.
Given:
Mass of the space probe, \( m = 95 \, \text{kg} \),
Acceleration due to gravity on the surface of the asteroid, \( g = 2.7 \times 10^{-3} \, \text{m/s}^2 \).
\[ \text{Weight} = 95 \, \text{kg} \times 2.7 \times 10^{-3} \, \text{m/s}^2 \]
\[ \text{Weight} = 95 \times 2.7 \times 10^{-3} \, \text{N} \]
\[ \text{Weight} = 256.5 \times 10^{-3} \, \text{N} \]
\[ \text{Weight} = 0.2565 \, \text{N} \]
So, the weight of the probe when close to the surface of the asteroid is \(0.2565 \, \text{N}\).
Question
(c) (i) As the probe approaches the surface of the asteroid, a rocket engine is fired to slow its descent. Explain how the engine changes the speed of the probe.[3]
▶️Answer/Explanation
Ans:
The rocket engine changes the speed of the probe by exerting a force on it in the opposite direction to its motion, in accordance with Newton’s third law of motion, which states that “for every action, there is an equal and opposite reaction.”
When the rocket engine is fired, it expels high-speed exhaust gases in one direction, generating a thrust force in the opposite direction according to Newton’s third law. This thrust force acts on the probe, causing it to accelerate in the direction opposite to the motion of the exhaust gases. As a result, the probe’s speed decreases, ultimately slowing its descent toward the surface of the asteroid.
In summary, the rocket engine changes the speed of the probe by exerting a thrust force in the opposite direction to its motion, causing it to decelerate and slow down.
Question
(ii) A constant force of \(12.0 \mathrm{~N}\) is exerted by the rocket engine. Determine the time for which the rocket must fire to reduce the speed of the probe from \(0.64 \mathrm{~m} \mathrm{~s}^{-1}\) to zero. State your answer to an appropriate number of significant figures.[4]
▶️Answer/Explanation
Ans:
Using the correct approach:
Given:
Net force on the probe: \(12.0 \, \text{N}\) exerted by the rocket engine, and \(0.26 \, \text{N}\) opposing the motion due to the gravitational force.
Mass of the probe: \(m = 95 \, \text{kg}\)
The net force on the probe is \(12.0 \, \text{N} – 0.26 \, \text{N} = 11.7 \, \text{N}\).
The acceleration of the probe is:
\[ a = \frac{F}{m} = \frac{11.7 \, \text{N}}{95 \, \text{kg}} \]
\[ a \approx 0.123 \, \text{m/s}^2 \]
Now, using the equation of motion:
\[ v = u + at \]
where \( v = 0 \, \text{m/s} \) (final velocity), \( u = 0.64 \, \text{m/s} \) (initial velocity), and \( a = 0.123 \, \text{m/s}^2 \) (acceleration).
\[ t = \frac{v – u}{a} = \frac{0 – 0.64}{0.123} \, \text{s} \]
\[ t \approx 5.2 \, \text{s} \]
So, the time for which the rocket must fire to reduce the speed of the probe from \(0.64 \, \text{m/s}\) to zero is approximately \(5.2 \, \text{s}\) when rounded to two significant figures.
Question
(d) As the probe lands, a small stone resting on a rock on the asteroid’s surface is projected horizontally from the top of the rock. The horizontal speed of the stone is \(34 \mathrm{~ms}^{-1}\) from a height of \(1.9 \mathrm{~m}\) above the surface of the asteroid.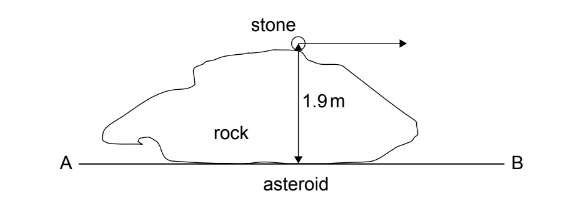
Estimate the horizontal distance from the stone’s point of projection along the line \(A B\) at which the stone lands. Ignore the curvature of the asteroid.[2]
▶️Answer/Explanation
Ans:
To estimate the horizontal distance from the stone’s point of projection along the line \(AB\) at which the stone lands, we can use the kinematic equation for horizontal motion:
\[d = v_x \cdot t\]
Given:
Horizontal speed of the stone, \(v_x = 34 \, \text{m/s}\)
Height of the stone above the surface, \(h = 1.9 \, \text{m}\)
First, let’s find the time \(t\) it takes for the stone to fall from a height of \(1.9 \, \text{m}\) above the surface. We can use the equation of motion for vertical motion:
\[h = \frac{1}{2} g t^2\]
Where:
\(g\) is the acceleration due to gravity (\(2.7 \times 10^{-3} \, \text{m/s}^2\))
Solving for \(t\):
\[t = \sqrt{\frac{2h}{g}}\]
\[t = \sqrt{\frac{2 \times 1.9}{2.7 \times 10^{-3}}}\]
\[t \approx \sqrt{1407.41}\]
\[t \approx 37.52 \, \text{s}\]
Now, we can find the horizontal distance \(d\) traveled by the stone:
\[d = v_x \cdot t\]
\[d = 34 \, \text{m/s} \times 37.52 \, \text{s}\]
\[d \approx 1275.68 \, \text{m}\]
So, the horizontal distance from the stone’s point of projection along the line \(AB\) at which the stone lands is approximately \(1275.68 \, \text{m}\).
