AP Calculus AB: 1.13 Removing Discontinuities - Exam Style questions with Answer- MCQ

AP PhysicsAP Calculus AP ChemistryAP Biology

Question

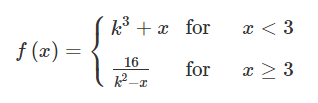
Let f be the function defined above, where k is a positive constant. For what value of k, if any, is f continuous?

A 2.081

B 2.646

C 8.550

D There is no such value of $k$

▶️Answer/Explanation

.Ans:A

The limit at $x equals 3$ exists if the left-hand and right-hand limits are equal. $\lim_{x\rightarrow 3^{-}}f(x)=\lim_{x\rightarrow 3^{+}}f(x)\Rightarrow k^{2}+3=\frac{16}{k^{2}-3}$ .The solution to this equation for $k greater than 0$ is $k equals 2.081$ . With this value of $k$ f(3) . Therefore, f is continuous at x=3

Question

Let f be the function given by $f(x)=\frac{2x^{2}+14x-16}{x^{2}-9x+8}$ For what values of x does f have a removable discontinuity?

A 1 only

B 8 only

C -8 and 1

D 1 and 8

▶️Answer/Explanation

Ans:A

Question

Let $f$ be the function defined above, where α is a constant. For what values of $a$ , if any, is $f$ continuous at $x equals 3$ ?

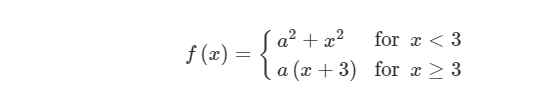
A 0 only

B 3 only

C 0 and 3

D There is no such a

▶️Answer/Explanation

Ans:B

$f$ is continuous at $x equals 3$ if $f of 3$ and both exist and are equal to each other.

$\lim_{x\rightarrow 3^{-}}f(x)=\lim_{x\rightarrow 3^{-}}(a^{2}+x^{2})$ =$a^{2}+3^{2}=a^{2}+9$

$\lim_{x\rightarrow 3^{+}}f(x)=\lim_{x\rightarrow 3^{+}}a(x+3)=$ a(3+3)=6a

f(3)=a(3+3)=6a Setting these equal to each other and solving for a yields the following. $a^{2}+9=6a\Rightarrow a^{2}-6a+9=0\Rightarrow (a-3)^{2}=0\Rightarrow a=3$

Question

Let f be the function given by$ f(x)=\frac{2x^{2}+14x-16}{x^{2}-9x+8}$ .For what values of x does f have a removable discontinuity?

A 1 only

B 8 only

C -8 and 1

D 1 and 8

▶️Answer/Explanation

Ans:A

AP Calculus AB: 1.13 Removing Discontinuities – Exam Style questions with Answer- MCQ

Question

Question

Question

Question

Need Help ? Book A Tutor