Question
The radius r of a sphere is increasing at the uniform rate of 0.3 inches per second. At the instant
when the surface area S becomes 100π square inches, what is the rate of increase, in cubic inches
per second, in the volume V ? \(\left ( S=4\pi r^{2} and V=\frac{4}{3}\pi r^{3} \right )\)
(A) 10π (B) 12π (C) 22.5π (D) 25π (E) 30π
▶️Answer/Explanation
Ans:D
Question
The area of a circular region is increasing at a rate of 96π square meters per second. When the area of the region is 64π square meters, how fast, in meters per second, is the radius of the region increasing?
(A) 6 (B) 8 (C) 16 (D)\(\sqrt[4]{3}\) (E)\(\sqrt[12]{3}\)
▶️Answer/Explanation
Ans:A
A\( =πr^2, A= 64π \) , when r = 8. Take the derivative with respect to t. \(\frac{dA}{dt}=2\pi r . \frac{dr}{dt};96\pi=2 \pi (8).\frac{dr}{dt}\Rightarrow \frac{dr}{dt}=6\)
Question
A spherical balloon is being inflated. What is the volume of the sphere at the instant when the rate of increase of the surface area is four times the rate of increase of the radius of the sphere?
(A) \(\frac{1}{2\pi }\) cubic units
(B) \(\frac{3\pi r^{2}}{2 }\) cubic units
(C) \(4\pi ^{2}\) cubic units
(D) \(\frac{1}{6\pi ^{2}}\) cubic units
▶️Answer/Explanation
Ans: (D)
Let V be the volume of the sphere, s be the surface area of the sphere, and r be the radius of the sphere. You are given that dS/dt = 4 dr/dt.
\(S=4\pi r^{2}\)
\(\frac{\mathrm{d} S}{\mathrm{d} t}=8\pi r\frac{\mathrm{d} r}{\mathrm{d} t}\)
\(\frac{\mathrm{d} S}{\mathrm{d} t}=4\frac{\mathrm{d} r}{\mathrm{d} t}(given)\)
\(8\pi r\frac{\mathrm{d} S}{\mathrm{d} t}=4\frac{\mathrm{d} r}{\mathrm{d} t}\)
\(2\pi r=1\)
\(r=\frac{1}{2\pi }\)
\(V=\frac{4}{3}\pi r^{3}\)
\(V=\frac{4}{3}\pi \left ( \frac{1}{2\pi } \right )^{3}\)
\(V=\frac{4}{3}\pi \left ( \frac{1}{8\pi ^{3}} \right )\)
\(V=\frac{1}{6\pi ^{2}}\)
Question
A conical funnel has a base diameter of 4 cm and a height of 5 cm. The funnel is initially full, but water is draining at a constant rate of \(2cm^{3}/s\). How fast is the water level falling when the water is 2.5 cm high?
(A) \(\frac{1}{2\pi}\) cm/s
(B) \(-\frac{1}{2\pi}cm/s\)
(C) \(\frac{2}{\pi }cm/s\)
(D)\(-\frac{2}{\pi } cm/s\)
▶️Answer/Explanation
Ans:(D)
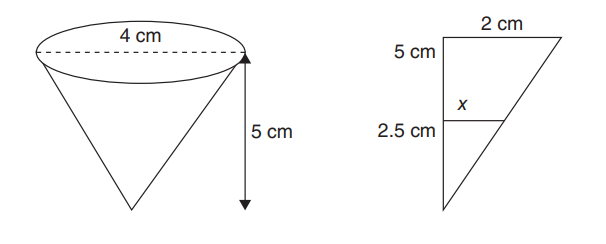
\(\frac{2}{5}=\frac{r}{r}\)(Similar triangles)
2h=5r
\(r=\frac{2h}{5}\)
\(V=\frac{1}{3}\pi r^{2}h\)
\(V=\frac{1}{3}\pi \left ( \frac{2h}{5} \right )^{2}h\)
\(V=\frac{1}{3}\pi \left ( \frac{4h^{2}}{25} \right )h\)
\(V=\frac{4}{75}\pi h^{3}\)
\(\frac{\mathrm{d} V}{\mathrm{d} t}=3\left ( \frac{4}{75} \right )\pi h^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\)
\(\frac{\mathrm{d} V}{\mathrm{d} t}=\left ( \frac{4}{25} \right )\pi h^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\)
\(\frac{\mathrm{d} V}{\mathrm{d} t}=-2cm^{3}/s\)
\(-2=\left ( \frac{4}{25} \right )\pi h^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\)
\(-1=\left ( \frac{2}{25} \right )\pi h^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=-\frac{25}{2\pi h^{2}}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=-\frac{25}{2\pi (2.5)^{2}}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=-\frac{2}{\pi }cm/s\)
