Question:
| t (minutes) | 0 | 4 | 9 | 15 | 20 |
| W (t) (degrees Fahrenheit) | 55.0 | 57.1 | 61.8 | 67.9 | 71.0 |
The temperature of water in a tub at time t is modeled by a strictly increasing, twice-differentiable function W, where W (t) is measured in degrees Fahrenheit and t is measured in minutes. At time t = 0, the temperature of the water is 550 F. The water is heated for 30 minutes, beginning at time t = 0. Values of W (t) at selected times t for the first 20 minutes are given in the table above.
(a) Use the data in the table to estimate W'(12) . Show the computations that lead to your answer. Using correct units, interpret the meaning of your answer in the context of this problem.
(b) Use the data in the table to evaluate \(\int_{0}^{20}W'(t)dt.\) Using correct units, interpret the meaning of \(\int_{0}^{20}W'(t)dt\) in the context of this problem.
(c) For 0 ≤ t ≤ 20, the average temperature of the water in the tub is \(\frac{1}{20}\int_{0}^{20}W(t)dt.\) Use a left Riemann sum with the four subintervals indicated by the data in the table to approximate \(\frac{1}{20}\int_{0}^{20}W(t)dt.\) Does this approximation overestimate or underestimate the average temperature of the water over these 20 minutes?
Explain your reasoning.
(d) For 20 ≤ t ≤ 25, the function W that models the water temperature has first derivative given by W'(t) \(= 0.4\sqrt{t }cos (0.06t).\) Based on the model, what is the temperature of the water at time t =25 ?
▶️Answer/Explanation
Ans:
(a)
\(W'(12)\approx \frac{67.9-61.8}{15-9}=1.0167 F/min\)
At t = 12, the temperature of the water in the tub is increasing at the rate of 1.0167 . F/min.
(b)
\(\int_{0}^{20}W'(t)dt = W(20)-W(0)=7.10-55.0 = 16^{0}F\)
\(\int_{0}^{20}W'(t)dt \) is the difference in temperature in 0F of the water in the tub at t = 20 and t = 0.
(c)
\(\int_{0}^{20}W(t)dt \approx 4(55.0)+5(57.1)+6(61.8)+5(67.9)\)
= 1215.8
\(\frac{1}{20}\int_{0}^{20}W(t)dt =60.79^{0}F\)
As the function W(t) is strictly increasing, the approximation rectangles of the left Riemann sum fall. below the curve. Thus the approximation is an under estimate.
(d)
\(\int_{20}^{25}W'(t)= W(25)-W(20)=2.043\)
W(25) – 71.0 = 2.043
W(25) = 73.0432 0F
Question:
The rate at which a baby bird gains weight is proportional to the difference between its adult weight and its current weight. At time t = 0, when the bird is first weighed, its weight is 20 grams. If B (t) is the weight of the bird, in grams, at time t days after it is first weighed, then
\(\frac{dB}{dt}= \frac{1}{5}(100-B).\)
Let y = B (t) be the solution to the differential equation above with initial condition B(0) = 20.
(a) Is the bird gaining weight faster when it weighs 40 grams or when it weighs 70 grams? Explain your reasoning.
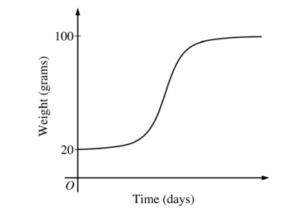
(b) Find \(\frac{d^{2}B}{dt^{2}}\) in terms of B. Use \(\frac{d^{2}B}{dt^{2}}\) to explain why the graph of B cannot resemble the following graph.
(c) Use separation of variables to find y = B(t), the particular solution to the differential equation with initial condition B(0) = 20.
▶️Answer/Explanation
Ans:
(a) When it is 40 grams : \(\frac{dB}{dt}=\frac{1}{5}(100-40)=12\) g/day
when it is 70 grams: \(\frac{dB}{dt}=\frac{1}{5}(100-70)=6\) g/day
So the bird is gaining weight faster when it weighs 40 grams.
(b)
\(\frac{dB}{dt}=20-\frac{1}{5}B\)
\(\frac{d^{2}B}{dt^{2}}=-\frac{1}{5}.\frac{dB}{dt}\)
\(=-\frac{1}{5}(20-\frac{1}{5}B)\)
\(=\frac{1}{25}B-4\)
\(\frac{1}{25}B-4>0\)
B > 100
So, the graph cannot be concave up when weight is below 100 g.
(c)
\(\frac{dB}{dt}=\frac{1}{5}(100-B)\)
\(\frac{1}{\frac{1}{5}(100-B)}dB = dt\)
\(\frac{1}{100-B}dB = dt\)
\(\int \frac{1}{100-B}dB = \int 1dt\)
-5 In [100-B] = t + c
\(In (100-B) = – \frac{1}{5}(t+c)\)
\(100-B = e^{- \frac{1}{5}(t+c)}\)
\(B = 100-e^{- \frac{1}{5}(t+c)}\)
\(20 = 100-e^{- \frac{1}{5}c}\)
\(e^{- \frac{1}{5}c}=80\)
\(- \frac{1}{5}c= ln 80\)
\(c = -5 ln 80\)
\(\partial B= 100-e^{- \frac{1}{5}c+-5 ln 80}\)
Question:
On a certain workday, the rate, in tons per hour, at which unprocessed gravel arrives at a gravel processing plant is modeled by \(G(t)=90+45 Cos\left ( \frac{t^{2}}{18} \right ),\) where t is measured in hours and 0 ≤ t ≤ 8. At the beginning of the workday (t = 0), the plant has 500 tons of unprocessed gravel. During the hours of operation,0 ≤ t ≤ 8 the plant processes gravel at a constant rate of 100 tons per hour.
(a) Find G’(5). Using correct units, interpret your answer in the context of the problem.
(b) Find the total amount of unprocessed gravel that arrives at the plant during the hours of operation on this workday.
(c) Is the amount of unprocessed gravel at the plant increasing or decreasing at time t = 5 hours? Show the work that leads to your answer.
(d) What is the maximum amount of unprocessed gravel at the plant during the hours of operation on this workday? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(G(t)=90+45 Cos\frac{t^{2}}{18}\)
\(G'(t)=-5t sin\left ( \frac{t^{2}}{18} \right )\)
G’(5) = – 24.588 tons/ hr2
This means that the rate at which unprocessed gravel arrives at the processing plant is changing by -24.588 tons per hour per hour, or decreasing by 24.588 tons per hour per hour, at t = 5 hours.
(b)
\(\int_{0}^{8}\left [ 90+45 cos\left ( \frac{t^{2}}{18} \right ) \right ]dt= 825.551 tons\)
(c)
Let V(t) be the amount of unprocessed gravel.
V’(t) is the rate of which the amount of unprocessed gravel is changing.
V’(t) = G(t) – 100
V’(5) = G(5) – 100
\(=90+45 cos \left ( \frac{52}{18} \right )-100\)
V’(5) = – 1.859
Since V’(5) is negative the amount of unprocessed gravel is decreasing at time t = 5 hours
(d)
V’(t) = 0 at t = ?
0 = G(t) – 100
\(100=90+45 cos \left ( \frac{t^{2}}{18} \right )\)
\(10=45 cos \left ( \frac{t^{2}}{18} \right )\)
T = 4.923
\(v(t)-v(0)=\int_{0}^{t}\left ( G(x)-100 \right )dx\)
\(v(t)=\int_{0}^{t}\left ( G(x)-100 \right )dx+v(0)\)
V (0) = 500
V(4.923) = 635.76
V(8) = 525.551
Since v(t) is on a closed interval [0, 8 ], the maximum amount must occur at an endpoint or at a critical value after evaluating the amount of unprocessed gravel at t = 0, t = 4.923, and t = 8, the amount of unprocessed gravel is highest at t = 4.923, with 635.376 tons of unprocessed gravel.
Question:
| t (minutes) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| C (t) (ounces) | 0 | 5.3 | 8.8 | 11.2 | 12.8 | 13.8 | 14.5 |
Hot water is dripping through a coffeemaker, filling a large cup with coffee. The amount of coffee in the cup at time t, 0 ≤ t ≤ 6, is given by a differentiable function C, where t is measured in minutes. Selected values of C (t), measured in ounces, are given in the table above.
(a) Use the data in the table to approximate C'(3.5) . Show the computations that lead to your answer, and indicate units of measure.
(b) Is there a time t, 2 ≤ t ≤ 4 at which C’ (t)= 2 ? Justify your answer.
(c) Use a midpoint sum with three subintervals of equal length indicated by the data in the table to approximate the value of \(\frac{1}{6}\int_{0}^{6}C(t)dt.\) Using correct units, explain the meaning of \(\frac{1}{6}\int_{0}^{6}C(t)dt\) in the context of the problem.
(d) The amount of coffee in the cup, in ounces, is modeled by \(B(t)= 16-16e^{-0.4t}\). Using this model, find the rate at which the amount of coffee in the cup is changing when t = 5.
▶️Answer/Explanation
Ans:
(a)
\(C'(3.5)\approx \frac{\left ( (4)-(3) \right )}{4-3}=\frac{12.8-11.2}{1}=1.6\frac{08}{min}\)
(b)
Since C(t) is differentiable for all values is [2, 4], we can say that there must be some value of t in (2, 4), such as t = a, such that \(C'(a)=\frac{\left ( (4)-(2) \right )}{4-2}=\frac{12.8-8.8}{2}=2\) by the mean value theorem
so, yes’.
(c)
\(\frac{1}{6}\int_{0}^{6}C(t)dt \approx \frac{1}{6}-2.(5.3+11.2+13.8)\)
≈ 10.1 0t
This is the average value, in oz, of the amount of coffee in the cup over the interval 0 ≤ t ≤ 6.
(d)
\(B'(t)= \frac{32}{5}e^{-0.4t}\)
\(B'(5)= \frac{32}{5}e^{-2}\)
Question:
t (minutes) | 0 | 2 | 5 | 8 | 12 |
vA (t) (meters/ minute) | 0 | 100 | 40 | -120 | -150 |
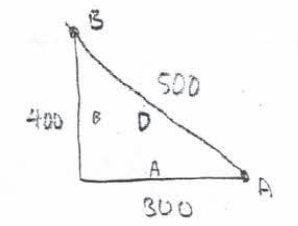
Train A runs back and forth on an east-west section of railroad track. Train A’s velocity, measured in meters per minute, is given by a differentiable function vA (t) where time t is measured in minutes. Selected values for vA (t) are given in the table above.
(a) Find the average acceleration of train A over the interval 2 ≤ t ≤ 8.
(b) Do the data in the table support the conclusion that train A’s velocity is -100 meters per minute at some time t with 5 < t < 8 ? Give a reason for your answer.
(c) At time t = 2, train A’s position is 300 meters east of the Origin Station, and the train is moving to the east. Write an expression involving an integral that gives the position of train A, in meters from the Origin Station, at time t = 12. Use a trapezoidal sum with three subintervals indicated by the table to approximate the position of the train at time t = 12.
(d) A second train, train B, travels north from the Origin Station. At time t the velocity of train B is given by vB (t) = -5t2 + 60t + 25, and at time t = 2 the train is 400 meters north of the station. Find the rate, in meters per minute, at which the distance between train A and train B is changing at time t = 2.
▶️Answer/Explanation
Ans:
(a)
\(\frac{v(8)-v(2)}{8-2}\rightarrow \frac{-120-100}{6}\rightarrow \frac{-220}{6}\rightarrow \frac{-110}{3}m/min^{2}\)
(b)
Yes, because v(8) = -120 and v(5) = 40 and the function is differentiable and this continuous the train’s velocity must be -100 m/min at some point between 5 < t < 8 accordingly to the intermediate value theorem.
(c)
\(x(12)= \int_{2}^{12}{v_{A}}^{(t)}dt + x(2)\rightarrow x(12)=\int_{2}^{12}{v_{A}}^{(t)}dt +300\)
\(x(12)\approx 3\cdot \frac{1}{2}\cdot (140)+3\cdot \frac{1}{2}\cdot (-80)+4\cdot \frac{1}{2}\cdot (-270)+300\)
210 – 120 – 540 + 300
210 – 240 – 120
-30-120
150 meaning it is 150 m W of origin station
(d)
\(\frac{dB}{dt}= -5t^{2}+60t + 25 \rightarrow 125 m/min\)
-20 + 120 +25
120 + 5 → 135
\(\frac{dA}{dt}= 100 m/min\)
A2 + B2 + = D2
\(2A\frac{dA}{dt}+2B\frac{dB}{dt}=2D\frac{dD}{dt}\)
600(100) + 800 (125) = 1000 \(\frac{dD}{dt}\)
6000 + 100000 = 1000 \(\frac{dD}{dt}\)
\(\frac{160,000}{1000}=\frac{dD}{dt}\rightarrow \frac{dD}{dt}=160 m/min\)
Question:
The rate at which rainwater flows into a drainpipe is modeled by the function R, where \(R(t)=20sin\left ( \frac{t^{2}}{35} \right )\) cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0.
(a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
(b) Is the amount of water in the pipe increasing or decreasing at time t = 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
▶️Answer/Explanation
Ans:
(a)
\(\int_{0}^{8}R(t)dt = \int_{0}^{8}20 sin\frac{t^{2}}{35}dt=76.570ft^{3}\)
During the eight hour interval, about 76.570 cubic feet of water flow into the drainpipe
(b)
Total water : T(x) \(T'(x) = R(x) – F(x) = 20in\frac{t^{2}}{35}+.04t.^{3}-.4t^{2}-.96t\)
T'(3) = 20 in 9/35 + .04(27) – .4(0) – .96(3) : : 314 < 0
after three hours, the amount of water in the pipe is decreasing because the derivative of the amount of water (the difference between water interring and leaving) is less than zero at 3 hours.
(c)
T'(t) = 0 @ t = 0, 3.2716584
\(T(t)=T(0)+\int_{0}^{t}T'(t)dt=30+\int_{0}^{t}T'(t)dt\)
T(0) = 30
T(3.272) = 27.965
T(8) = 48.544
after testing all critical numbers and endpoints for their values, the amount of water in the pipe achieves a minimum value of about 27.965 after about 3.272 hours.
(d)
50 = T(w)
\(50 = 30+\int_{0}^{w}T'(t)dt\)
\(20 = \int_{0}^{w}T'(t)dt=\int_{0}^{w}\left [ R(t)-D(t) \right ]dt\)
Question:
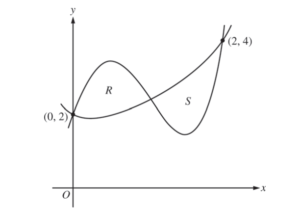
Let f and g be the functions defined by \(f(x)= 1 + x + e^{x^{2}-2x}\) and g(x) = x4 – 6.5x2 + 6x + 2. Let R and S be the two regions enclosed by the graphs of f and g shown in the figure above.
(a) Find the sum of the areas of regions R and S.
(b) Region S is the base of a solid whose cross sections perpendicular to the x-axis are squares. Find the volume of the solid.
(c) Let h be the vertical distance between the graphs of f and g in region S. Find the rate at which h changes with respect to x when x = 1.8.
▶️Answer/Explanation
Ans:
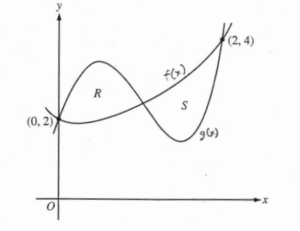
(a)
f(a) = g(a)
a = 1.0328318883641
\(\int_{0}^{9}\left [ g(x)-f(x) \right ]dx+\int_{0}^{2}\left [ f(x)-g(x) \right ]dx=2.004\)
(b)
Cross sation area A(x) = (f(x) – g(x))2 a = 1.0328318883641
\(\int_{2}^{9}A(x)dx=1.283\)
(c)
f'(1.8) = 2.1162821217136
g'(1.8) = 5.928
\(\frac{dh}{dx}=f'(1.8)-g'(1.8)=-3.812\)
Question:
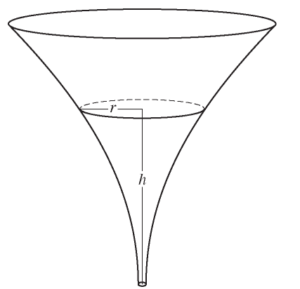
The inside of a funnel of height 10 inches has circular cross sections, as shown in the figure above. At height h, the radius of the funnel is given by \(r = \frac{1}{20}\left ( 3+h^{2} \right ),\) where 0 ≤ h ≤ 10. The units of r and h are inches.
(a) Find the average value of the radius of the funnel.
(b) Find the volume of the funnel.
(c) The funnel contains liquid that is draining from the bottom. At the instant when the height of the liquid is h = 3 inches, the radius of the surface of the liquid is decreasing at a rate of \(\frac{1}{5}\) inch per second. At this instant, what is the rate of change of the height of the liquid with respect to time?
▶️Answer/Explanation
Ans:
(a)
\(r_{avg}= \frac{1}{200}\int_{0}^{10}\left ( 3+h^{2} \right )dh\)
\(= \frac{1}{200}\left ( 3h+\frac{h^{3}}{3} \right )_{0}^{10}\textrm{]}\)
\(= \frac{1}{200}\left ( 30+\frac{1000}{3} \right )\)
\(= \frac{109}{60} inches.\)
(b)
\(v = \frac{\pi }{400}\int_{0}^{10}(3+h)^{2}dh\)
\(= \frac{\pi }{400}\int_{0}^{10}(9+6h^{2}+h^{4})dh\)
\(= \frac{\pi }{400}(9h+2h^{3}+\frac{h^{5}}{5})_{0}^{10}\textrm{]}\)
\(= \frac{\pi }{400}(90+2000+20000)\)
\(= \frac{2209\pi }{40}in^{3}\)
(c)
\(r = \frac{1}{20}(3+h^{2})\)
\(\frac{dr}{dt}= \left ( \frac{h}{10} \right )\frac{dh}{dt}\)
\(-\frac{1}{5}= \frac{3}{10}\frac{dh}{dt}\)
\(\frac{dh}{dt}= -\frac{2}{3}\) inch per second
Question:
| t (hours) | 0 | 1 | 3 | 6 | 8 |
| R (t) (liters / hour) | 1340 | 1190 | 950 | 740 | 700 |
Water is pumped into a tank at a rate modeled by \(W(t)= 2000e^{-t^{2}/20}\) liters per hour for 0 ≤ t ≤ 8, where t is measured in hours. Water is removed from the tank at a rate modeled by R (t) liters per hour, where R is differentiable and decreasing on 0 ≤ t ≤ 8. Selected values of R (t) are shown in the table above. At time t 0, there are 50,000 liters of water in the tank.
(a) Estimate R'(2). Show the work that leads to your answer. Indicate units of measure.
(b) Use a left Riemann sum with the four subintervals indicated by the table to estimate the total amount of water removed from the tank during the 8 hours. Is this an overestimate or an underestimate of the total amount of water removed? Give a reason for your answer.
(c) Use your answer from part (b) to find an estimate of the total amount of water in the tank, to the nearest liter, at the end of 8 hours.
(d) For 0 ≤ t ≤ 8, is there a time t when the rate at which water is pumped into the tank is the same as the rate at which water is removed from the tank? Explain why or why not.
▶️Answer/Explanation
Ans:
(a)
\(R'(2)\approx \frac{R(3)-R(1)}{3-1}=\frac{950-1190}{2}\)
R'(2) ≈ -120 L/hr2
(b)
\(\int_{0}^{8}R(t)dt\approx L_{4}=(1)(1340)+(2)(1190)+(3)(950)+(2)(740)\)
\(\int_{0}^{8}R(t)dt\approx 8,050 L\)
This is an underestimate because we are taking the left Riemann sum of a decreasing function. Therefore the left endpoints are greater than the right endpoints in each subinterval.
(c)
t = + 50, 000 L
Total left ≈ 50,000 + \(\left ( \int_{0}^{8}W(t)dt – \int_{0}^{8}R(t)dt \right )\)
\(\int_{0}^{8}W(t)dt = 7836.19532455\)
Total left ≈ 50,000 + (7836.19332455-8050)
Total left ≈ 49,786 L
(d)
T(t) = W(t) – R(t)
T(0) = 2000 – 1340 = 600 -648.47 < 0 < 600
T(8) = 81.524-700 = -618.47
When T(t) = 0, the rate of water being pumped in to the tank is equal to the rate of water being pumped out. Because the function T(t) is continuous and differentiable by IVT these exists some t on the interval [0, 8] where T(t) = 0.
Question:
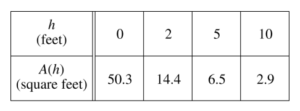
A tank has a height of 10 feet. The area of the horizontal cross section of the tank at height h feet is given by the function A, where A (h) is measured in square feet. The function A is continuous and decreases as h increases. Selected values for A (h) are given in the table above.
(a) Use a left Riemann sum with the three subintervals indicated by the data in the table to approximate the volume of the tank. Indicate units of measure.
(b) Does the approximation in part (a) overestimate or underestimate the volume of the tank? Explain your reasoning.
(c) The area, in square feet, of the horizontal cross section at height h feet is modeled by the function f given by \(f(h)=\frac{50.3}{e^{0.2h}+h}\) Based on this model, find the volume of the tank. Indicate units of measure.
(d) Water is pumped into the tank. When the height of the water is 5 feet, the height is increasing at the rate of 0.26 foot per minute. Using the model from part (c), find the rate at which the volume of water is changing with respect to time when the height of the water is 5 feet. Indicate units of measure.
▶️Answer/Explanation
Ans:
(a)
v ≈ [2(50.3) + 3 (14.4) + 5(6.5)]
≈ 176.3 ft3
(b)
The approximation in part a is an overestimate because A is a decreasing function.
(c)
\(v=\int_{0}^{10}\left ( \frac{50.3}{e^{0.2h}+h} \right )dh\)
≈ 101.325 ft3
(d)
h = 5 ft
\(\frac{dh}{dt}= 0.26 ft/min\)
\(\frac{dv}{dt}= ?\)
\(v=\int_{0}^{h}\left ( \frac{50.3}{e^{0.2h}+h} \right )dh\)
\(\frac{dv}{dt}= \frac{50.3}{e^{0.2h}+h}\cdot \frac{dh}{dt}\)
\( =\frac{50.3}{e^{0.2(5)}+(5)}\cdot 0.26\)
≈ 1.694 ft3/min
Question:
When a certain grocery store opens, it has 50 pounds of bananas on a display table. Customers remove bananas from the display table at a rate modeled by
\(f(t)=10+(0.8t)sin\left ( \frac{t^{3}}{100} \right )\) for 0 < t ≤ 12,
where f ( t) is measured in pounds per hour and t is the number of hours after the store opened. After the store has been open for three hours, store employees add bananas to the display table at a rate modeled by
g(t) = 3 + 2.4 In (t2 + 2t) for 3 < t ≤ 12,
where g (t) is measured in pounds per hour and t is the number of hours after the store opened.
(a) How many pounds of bananas are removed from the display table during the first 2 hours the store is open?
(b) Find f'(7) . Using correct units, explain the meaning of f'(7) in the context of the problem.
(c) Is the number of pounds of bananas on the display table increasing or decreasing at time t = 5 ? Give a reason for your answer.
(d) How many pounds of bananas are on the display table at time t = 8 ?
▶️Answer/Explanation
Ans:
(a)
\(\int_{0}^{2}f(t)dt = 20.051\) lbs.
(b)
f'(7) = -8.119 lbs. per hour2
At time t = 7, the rate at which customers remove bananas from the display table is decreasing at a rate of 8.119 lbs. per hour per hour.
(c)
f(5) = 13.796
g(5) = 11.532
The number of pounds of bananas on the display table is decreasing at time t = 5, because f(5) > g(5).
(d)
\(50 – \int_{0}^{8}f(t)dt+\int_{3}^{8}g(t)dt=23.347\) lbs.
Question:
Fish enter a lake at a rate modeled by the function E given by \(E(t)=20 + 15 sin\left ( \frac{\pi t}{6} \right ).\) Fish leave the lake at a rate modeled by the function L given by L(t) = 4 + 20.1t2. Both E (t) and L (t) are measured in fish per
hour, and t is measured in hours since midnight (t = 0).
(a) How many fish enter the lake over the 5-hour period from midnight (t = 0) to 5 A.M. (t = 5) ? Give your answer to the nearest whole number.
(b) What is the average number of fish that leave the lake per hour over the 5-hour period from midnight (t = 0) to 5 A.M. (t = 5) ?
(c) At what time t, for 0 ≤ t ≤ 8, is the greatest number of fish in the lake? Justify your answer.
(d) Is the rate of change in the number of fish in the lake increasing or decreasing at 5 A.M. (t = 5) ? Explain your reasoning.
▶️Answer/Explanation
Ans:
(a)
\(\int_{0}^{5}E(t)dt\approx 153 fish\)
(b)
\(\frac{1}{5}\int_{0}^{5}L(t)dt\approx \frac{30.295}{5}\approx 6.059\) fish per hour leave the lake
(c)
E(t) – L(t) = 0
t ≈ 6.204
E(t) – L(t) is the rate at which the number of fish is changing
At time t = 6.204, the greatest number of fish in the 8 hour period are in the lake. This is because E(t) – L(t) is positive from t = 0 + 0 t = 6.204 indicating that the number of fish in the lake is increasing over (0, 3.204), but E(t) – L(t) is negative from t = 6.204 to t = 8, which means the number of fish are decreasing in this time period, so the number of fish in the lake is greatest at t = 6.204 hours
(d)
\(\frac{d}{dt}\left ( 16+15 sin(\frac{\pi t}{6})-2^{0.1t2} \right )|_{t=5}\approx -10.723 fish / hour^{2}\)
Since the derivative of E(t) – L(t) at t = 5 is negative, the rate of change in the number of fish in the lake is decreasing
Question:
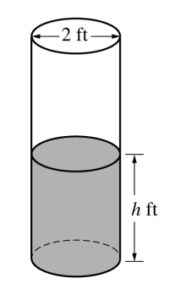
A cylindrical barrel with a diameter of 2 feet contains collected rainwater, as shown in the figure above. The water drains out through a valve (not shown) at the bottom of the barrel. The rate of change of the height h of the water in the barrel with respect to time t is modeled by \(\frac{dh}{dt}=-\frac{1}{10}\sqrt{h},\) where h is measured in feet and t is measured in seconds. (The volume V of a cylinder with radius r and height h is V = πr2h.)
(a) Find the rate of change of the volume of water in the barrel with respect to time when the height of the water is 4 feet. Indicate units of measure.
(b) When the height of the water is 3 feet, is the rate of change of the height of the water with respect to time increasing or decreasing? Explain your reasoning.
(c) At time t = 0 seconds, the height of the water is 5 feet. Use separation of variables to find an expression for h in terms of t.
▶️Answer/Explanation
Ans:
(a)
h = 4
\(\frac{dh}{dt}=\frac{-1}{10}\sqrt{4}=\frac{-1}{5}\) \(\frac{dv}{dt}=\pi \left [ r^{2}\frac{dh}{dt}+h(2r)\left ( \frac{dr}{dt} \right ) \right ]\)
\(\frac{dv}{dt}=?\) \(\frac{dv}{dt}=\pi \left [ (1)\left ( \frac{-1}{5} \right )+(4)(2)(0) \right ]\)
r = 1
\(\frac{dv}{dt}=0\) \(\frac{dv}{dt}=\frac{-\pi }{5}ft^{3}/sec\)
(b)
h = 3
\(\frac{d^{2}h}{dt^{2}}=?\) \(\frac{d^{2}h}{dt^{2}}=\frac{-1}{20}h^{-1/2}\frac{dh}{dt}=\frac{-1}{20\sqrt{3}}\left ( \frac{-1}{10}\sqrt{3} \right )=\frac{1}{200}\)
\(\frac{-1}{10}h^{1/2}\) The rate of change of height is increasing since \(\frac{d^{2}h}{dt^{2}}\) at h = 3 is positive.
1/20
(c)
\(\int h^{-1/2}dh=\int \frac{-1}{10}dt\)
\(\int h^{1/2}=\frac{-1}{10}t+c_{1}\)
\(h^{1/2}=\frac{-1}{20}t+c_{2}\)
\(h=\left ( \frac{-1}{20}t+c \right )^{2}\)
\(5=\left ( \frac{-1}{20}(0)+c \right )^{2}\)
\(c = \sqrt{5}\)
\(h = \left ( \frac{-1}{20}t+\sqrt{5} \right )^{2}\)
Question:
A medication is administered to a patient. The amount, in milligrams, of the medication in the patient at time t hours is modeled by a function y = A(t ) that satisfies the differential equation \(\frac{dy}{dt}=\frac{12-y}{3}.\) At time t = 0 hours, there are 0 milligrams of the medication in the patient.
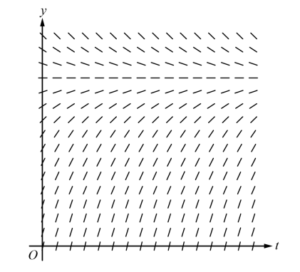
(a) A portion of the slope field for the differential equation \(\frac{dy}{dt}=\frac{12-y}{3}\) is given below. Sketch the solution curve through the point (0, 0).
(b) Using correct units, interpret the statement \(\lim_{t\rightarrow \infty }A(t)=12\) in the context of this problem.
(c) Use separation of variables to find y = A(t), the particular solution to the differential equation \(\frac{dy}{dt}=\frac{12-y}{3}\) with initial condition A(0) = 0.
(d) A different procedure is used to administer the medication to a second patient. The amount, in milligrams, of the medication in the second patient at time t hours is modeled by a function y = B(t) that satisfies the differential equation \(\frac{dy}{dt}=3 – \frac{y}{t+2}.\) At time t = 1 hour, there are 2.5 milligrams of the medication in the second patient. Is the rate of change of the amount of medication in the second patient increasing or decreasing at time t = 1 ? Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a)
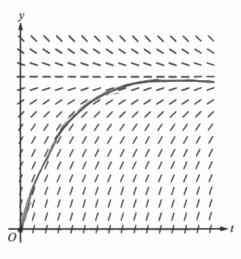
(b)
As time goes to infinity, the amount of medication in the patient, in milligrams, is approaching 12.
(c)
\(\frac{dy}{dt}=\frac{12-y}{3}\)
\(\int \frac{dy}{12-y}=\int \frac{dt}{3}\)
\(-en|12-y| = \frac{1}{3}t+c\) \(-en|12-y| = \frac{1}{3}t-en 12\)
\(-en|12-0| = \frac{1}{3}(0)+c\) \(en|12-y| = \frac{1}{3}t+en 12\)
c = -en 12 \(e^{en|12-y|} = e^{-\frac{1}{3}t+en 12}\)
\(12-y = e^{-\frac{1}{3}t}.e^{en 12}\)
\(12-y = 12e^{-\frac{1}{3}t}\)
\(-y = 12e^{-\frac{1}{3}t}-12\)
\(y = -12e^{-\frac{1}{3}t}+12\)
(d)
\(\frac{dy}{dt}=3 – \frac{y}{t+2}\)
\(\frac{d^{2}y}{dt^{2}}=-\frac{dy/dx(t+2)-1(y)}{(t+2)^{2}}\)
\(\frac{d^{2}y}{dt^{2}}=-\frac{\left ( 3-\frac{y}{t+2} \right )(t+2)-y}{(t+2)^{2}}\)
\(\frac{d^{2}y}{dt^{2}}|_{(1, 2.5)}=-\frac{\left ( 3-\frac{2.5}{1+2} \right )(1+2)-2.5}{(1+2)^{2}}=\frac{\left ( 3-\frac{5}{3} \right )(3)-2.5}{3^{2}}=\sim \) #
Question:
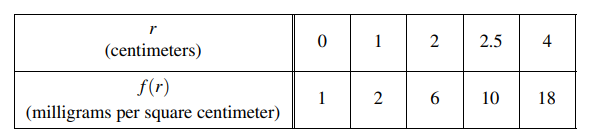
The density of a bacteria population in a circular petri dish at a distance r centimeters from the center of the dish is given by an increasing, differentiable function f , where f (r) is measured in milligrams per square centimeter. Values of f (r) for selected values of r are given in the table above.
(a) Use the data in the table to estimate f'(2.25). Using correct units, interpret the meaning of your answer in the context of this problem.
(b) The total mass, in milligrams, of bacteria in the petri dish is given by the integral expression \(2\pi \int_{0}^{4}r f(r)dr.\) Approximate the value of \(2\pi \int_{0}^{4}r f(r)dr\) using a right Riemann sum with the four subintervals indicated by the data in the table.
(c) Is the approximation found in part (b) an overestimate or underestimate of the total mass of bacteria in the petri dish? Explain your reasoning.
(d) The density of bacteria in the petri dish, for 1 ≤ r ≤ 4, is modeled by the function g defined by \(g(r)=2-16(cos (1.57\sqrt{r}))^{3}.\) For what value of k , 1 < k < 4, is g (k) equal to the average value of g (r) on the interval 1 ≤ r ≤ 4 ?
▶️Answer/Explanation
Ans:
(a)
\(f'(2.25)\approx \frac{f(2.5)-f(2)}{2.5-2}=\frac{10-6}{0.5}=\frac{4}{0.5}=8\) milligrams per square centimeter per centimeters.
The density of bacteria changes at a rate of approximately 8 milligrams per square centimeter per centimeter at distance r = 2.25 centimeters. From the center of the dish
(b)
\(2\pi \int_{0}^{9}r\cdot f(r)dr\approx 2\pi \cdot (2.1-1+6.1.2+10.0.5.2.5+18.1.5.4)\)
\(2\pi (2+12+12.5+108)=2\pi (13+.5)=269\pi milligrams\)
(c)
As a rule, Right Riemann sums are always an over estimate for functions with positive slove, and underestimates for functions with negative slope. The slope of r.f(r) is equal to r’.f(r) +r.f'(r). Since r, r’, f(r), and f'(r) are always positive on the internal [0, 4], r.f(r) always has a positive slope on that internal. Since it’s a positive sloped functions, the right Riemann sum for r.f(r) from 0 to 9 is an over estimate.
(d)
Avg of g(r) \(=\frac{1}{4-1}\int_{1}^{4}(2-16(cos(1.57\sqrt{r}))^{3})dr=\frac{29.627}{3}=9.876\)
\(g(k)= 2 – 16 (cos(1.57\sqrt{k}))^{3}=9.876\)
k = 2.497
