Question
If
is a function that has a removable discontinuity at x=3, which of the following could be the graph of f ?
A 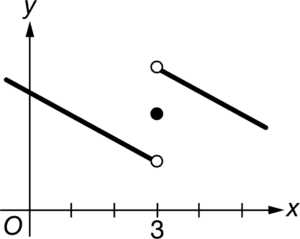
B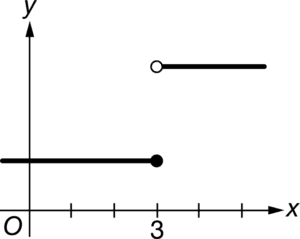
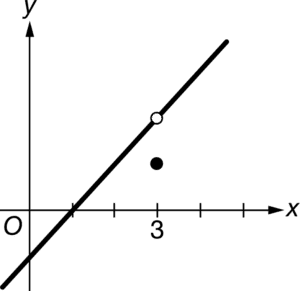
D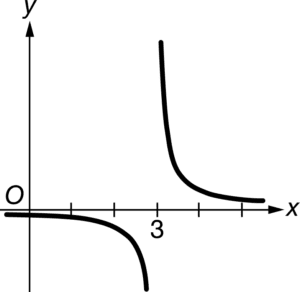
▶️Answer/Explanation
Ans:C
A removable discontinuity occurs at x=c if exists, but f(c)
does not exist or is not equal to the value of the limit. This graph could be the graph of f since ![]() exists but is not equal to f(3).
exists but is not equal to f(3).
Question
Paint spills onto a floor in a circular pattern. The radius of the spill increases at a constant rate of 2.5 inches per minute. How fast is the area of the spill increasing when the radius of the spill is 18 inches?
A \(5\pi in^{2}min^{-1}\)
B \(36\pi in^{2}min^{-1}\)
C \(45\pi in^{2}min^{-1}\)
D \(90\pi in^{2}min^{-1}\)
▶️Answer/Explanation
Ans:D
The area of the spill at time t is \(A=\pi r^{2}\) where r is the radius at time t and is measured in inches and t is measured in minutes. The goal of this related rates problem is to find the value of \(\frac{\mathrm{d} A}{\mathrm{d} t}\) at the moment when r=18 and \(\frac{\mathrm{d} r}{\mathrm{d} t}=2.5\)inches per minute. By the chain rule, \(\frac{\mathrm{d} A}{\mathrm{d} t}=2\pi r\frac{\mathrm{d} r}{\mathrm{d} t}=2\pi (18)(2.5)\) =\(90\pi in^{2}min^{-1}\)
Question
The radius of a circle is increasing. At a certain instant, the rate of increase in the area of the circle is numerically equal to twice the rate of increase in its circumference. What is the radius of the circle at that instant?
A \(\frac{1}{2}\)
B 1
C \(\sqrt{2}\)
D 2
E 4
▶️Answer/Explanation
Ans:D
Question
Functions w, x, and y are differentiable with respect to time and are related by the equation \(w=x^{2}y\) If x is decreasing at a constant rate of 1 unit per minute and y is increasing at a constant rate of 4 units per minute, at what rate is w changing with respect to time when x=6 and y=20?
A -384
B -240
C -96
D 276
E 384
▶️Answer/Explanation
Ans:C
