Question:
Let f be the function defined by f(x) = ex cos x.
(a) Find the average rate of change of f on the interval 0 ≤ x ≤ π .
(b) What is the slope of the line tangent to the graph of f at \(x = \frac{3\pi }{2}?\)
(c) Find the absolute minimum value of f on the interval 0 ≤ x ≤ 2π. Justify your answer.
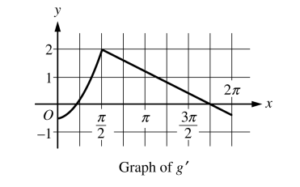
(d) Let g be a differentiable function such that \(g\left ( \frac{\pi }{2} \right )=0.\) The graph of g’, the derivative of g, is shown below. Find the value of \(\lim_{x\rightarrow \pi /2}\frac{f(x)}{g(x)}\) or state that it does not exist. Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(\frac{\int_{0}^{r}f'(x)dx}{r}=\frac{f(r)-f(0)}{r}=\frac{e^{r}cosr-e^{0}cos 0}{r}\)
\(\frac{e^{r}(-1)-1(1)}{r}=\frac{-e^{r}-1}{r}\)
(b)
\(\frac{df}{dx}=e^{x}cos x + e^{x}(-sinx)\)
\(=e^{x}(cos x -sinx)\)
\(=e^{3r/2}(0-(-1))=e^{3r/2}\)
(c)
from part B
\(f'(x)=e^{x}(cos x – sin x)= 0 \rightarrow e^{x}=0\) or cox = sin x \(x = \frac{\pi }{4},\frac{5\pi}{4}\)
Minima either have a derivative at 0, undefined, or are boundary points.
So possible values : x = 0, x = 2π, x = π/4 x = 5π/4
f(x) = 1 f(x) = e2π \(f(x)=e^{\pi /4}\left ( \frac{\sqrt{2}}{2} \right )\) \(f(x)=e^{5\pi /4}\left ( -\frac{\sqrt{2}}{2} \right )\)
Since \(e^{5\pi /4}\left ( -\frac{\sqrt{2}}{2} \right )\) is the only negative value of f(x), the absolute minimum of f(x) on 0 ≤ x ≤ 2π is \(-\frac{\sqrt{2}}{2}e^{5\pi /4}\) .
(d)
Note \(\lim_{x\rightarrow \frac{\pi }{2}}(g(x))=0\) since g(x) is differentiable (and thus continuous), and \(g\left ( \frac{\pi }{2} \right )=0.\) Also \(f\left ( \frac{\pi }{2} \right )=e^{\pi /2}\left ( cos\left ( \frac{\pi }{2} \right ) \right )=e^{\pi /2}(0)=0,\) and f(x) is continuous, So \(\lim_{x\rightarrow \frac{\pi }{2}}f(x)=0.\) So by L’ Hopital’s rule,
\(\lim_{x\rightarrow \frac{\pi }{2}}\left ( \frac{f(x)}{g(x)} \right )=\lim_{x\rightarrow \frac{2 }{2}}\left ( \frac{f'(x)}{g'(x)} \right )=\frac{e^{\pi /2}\left ( cos\frac{\pi }{2}-sin\frac{\pi }{2} \right )}{2}=\frac{-e^{\pi /2}}{2}\)
Question:
Functions f, g, and h are twice-differentiable functions with g(2) = h(2) = 4. The line \(y = 4+\frac{2}{3}(x-2)\) is tangent to both the graph of g at x = 2 and the graph of h at x = 2.
(a) Find h'(2).
(b) Let a be the function given by a(x) = 3x3h(x). Write an expression for a'(x). Find a'(2).
(c) The function h satisfies \(h(x)=\frac{x^{2}-4}{1-(f(x))^{3}}\) for x ≠ 2. It is known that \(\lim_{x\rightarrow 2}h(x)\) can be evaluated using L’Hospital’s Rule. Use \(\lim_{x\rightarrow 2}h(x)\) to find f(2) and f'(2 ). Show the work that leads to your answers.
(d) It is known that g(x) ≤ h(x) for 1 < x < 3. Let k be a function satisfying g(x) ≤ k(x) ≤ h(x) for 1 < x < 3. Is k continuous at x = 2 ? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(y = \frac{2}{3}(x-2)+4\)
point (2, 4) slope 2/3
h'(2) = 2/3
(b)
a'(x) = h'(x).3x3 + 9x2 h(x)
a'(2) = h'(2) . 3(2)3 + 9(2)2 h(2)
\(a'(2)=\frac{2}{3}\cdot 3\cdot 2^{3}+9\cdot 2^{2}\cdot 4\)
(c)
\(\lim_{x\rightarrow 2}\frac{x^{2}-4}{1-(f(x))^{3}}= \lim_{x\rightarrow 2}\frac{2x}{-3(f(x))^{2}.f'(x)}\) h (2) = 4
\(\therefore \lim_{x\rightarrow 2} h(x)\) must equal 4
\(\therefore \lim_{x\rightarrow 2} x^{2}-4=0\)
\( \lim_{x\rightarrow 2} 1-(f(x))^{3}=0\) if f(2) = 1 \(=\frac{2(2)}{-3(1)^{2}\cdot f'(2)}\)
∴ Indeterminate form 0/0 \(=\frac{4}{-3\cdot f'(2)}\) f'(2) must equal -1/3 so that \(\lim_{x\rightarrow 2} h(x) = 4\)
and L’Hopital’s rule applies \(=\frac{4}{-3\cdot -1/3}\)
Such that f(2) = 1 = 4/1
\(\lim_{x\rightarrow 2} h(x) = 4\) such that f(2) = 1 and f'(2) = -1/3
(d)
2 and h given as twice – differentiable ∴ g and h are continuous for 1 < x < 3
g(x) ≤ k(x) ≤ h(x)
\(\lim_{x\rightarrow 2} g(x) = 4\) because g continuous and g(2) = 4
\(\lim_{x\rightarrow 2} h(x) = 4\) because h continuous and h(2) = 4
By squeeze theorem, \(\lim_{x\rightarrow 2} k(x) = 4\)
k is between or equal to g and h for 1 < x < 3, given g(2) = 4 h (2) , meaning k(2) must equal 4, and \(\lim_{x\rightarrow 2} k(x) = 4\) so k(x) is continuous at x = 2
Question:
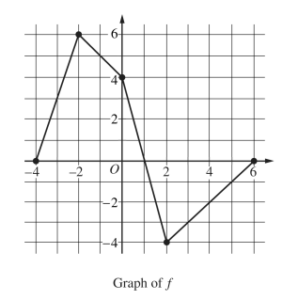
Let f be a continuous function defined on the closed interval −4 ≤ x ≤ 6. The graph of f , consisting of four line segments, is shown above. Let G be the function defined by \(G(x)=\int_{0}^{x}f(t)dt.\)
(a) On what open intervals is the graph of G concave up? Give a reason for your answer.
(b) Let P be the function defined by P (x) = G (x)• f(x). Find P'(3 ).
(c) Find \(\lim_{x\rightarrow 2}\frac{G(x)}{x^{2}-2x}.\)
(d) Find the average rate of change of G on the interval [−4, 2]. Does the Mean Value Theorem guarantee a value c, −4 < c < 2, for which G'(c) is equal to this average rate of change? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
G'(x) = f(x)
G”(x) = f'(x)
On (-4, -2) and (2, 6), G(x) is concave up because f(x) (which is equal to G'(x)) has a positive slope / is increasing.
(b)
p'(x) = G'(x) f(x) + f'(x) G(x)
p'(3) = G'(3) f(3) + f'(3) G(3)
G'(x) = f(x) \(G(3)=\int_{0}^{3}f(t)dt=-\frac{7}{2}\)
\(p'(3)=(-3)(-3)+(1)\left (- \frac{7}{2} \right )\)
(c)
\(\lim_{x\rightarrow 2}G(x)=\lim_{x\rightarrow 2}(x^{2}-2x)=0\) Must be I’hopital’s rule
\(\int_{0}^{2}f(t)dt=0\)
\(\lim_{x\rightarrow 2}\frac{G'(x)}{2x-2}=\frac{f(2)}{4-2}=\frac{-4}{2}\)
(d)
\(\int_{0}^{2}f(t)dt\) \(\int_{0}^{-4}f(t)dt= -(3+9+3+1)\)
= -16
AROC of \(G = \frac{G(2)-G(-4)}{2-(-4)}=\frac{0-(16)}{2+4}=\frac{16}{6}=\frac{8}{3}\)
The meanvalue theorem does guarantee a value of -4<c<2, for which G'(c) is equal to average rate of chang. This is because G'(x) = f(t) and x = t exists for all values, -4<x=+t<2, meaning that G(x) is continuous on the closed interval and differentiable on the open interval.
Question
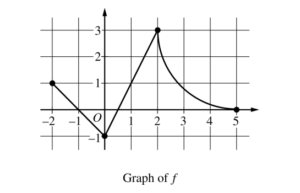
The continuous function f is defined on the closed interval −6 ≤ x ≤ 5. The figure above shows a portion of the graph of f, consisting of two line segments and a quarter of a circle centered at the point (5, 3). It is known that the point \(\left ( 3,3-\sqrt{5} \right )\) is on the graph of f.
(a) If \(\int_{-6}^{5}f(x)dx=7,\) find the value of \(\int_{-6}^{-2}f(x)dx\) Show the work that leads to your answer.
(b) Evaluate \(\int_{3}^{5}(2f'(x)+4)dx.\)
(c) The function g is given by \(\int_{-2}^{x}f(t)dt.\) Find the absolute maximum value of g on the interval − ≤ x ≤ 52 . Justify your answer.
(d) Find \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}.\)
▶️Answer/Explanation
Ans:
(a) \(\int_{-6}^{5}f(x)dx=\int_{-6}^{-2}f(x)dx+\int_{-2}^{5}f(x)dx\)
\(\Rightarrow 7=\int_{-6}^{-2}f(x)dx+2+\left ( 9-\frac{9\pi }{4} \right )\)
\(\Rightarrow \int_{-6}^{-2}f(x)dx=7-\left ( 11-\frac{9\pi }{4} \right )=\frac{9\pi }{4}-4\)
(b) \(\int_{3}^{5}(2f'(x)+4)dx=2\int_{3}^{5}f'(x)+\int_{3}^{5}4dx\)
= 2 (f(5)- f(3)) + 4 (5-3)
\(=2(0-(3-\sqrt{5}))+8\)
\(=2(-3+\sqrt{5})+8=2+2\sqrt{5}\)
-OR-
\(\int_{3}^{5}(2f'(x)+4)dx=_{x=3}[2f(x)+4x]^{x=5}\)
=(2f(5) + 20) – (2 f(3) + 12)
\(=(2.0+20)-(2(3-\sqrt{5})+12)\)
\(=2+2\sqrt{5}\)
(c) \(g'(x)=f(x)=0\Rightarrow x=-1, x=\frac{1}{2}, x=5\)
| x | g(x) |
-2 -1 \(\frac{1}{2}\) 5 | 0 \(\frac{1}{2}\) \(-\frac{1}{4}\) \(11-\frac{9\pi }{4}\) |
On the interval -2 ≤ x ≤ 5, the absolute maximum value of g is g(5) = \(11-\frac{9\pi }{4}.\)
(d) \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}=\frac{10^{1}-3f'(1)}{f(1)-arctan 1}\)
\(=\frac{10-3.2}{1-arctan 1}=\frac{4}{1-\frac{\pi }{4}}\)
Question
| t (minutes) | 0 | 4 | 9 | 15 | 20 |
| W(t) (degrees Fahrenheit) | 55.0 | 57.1 | 61.8 | 67.9 | 71.0 |
The temperature of water in a tub at time t is modeled by a strictly increasing, twice-differentiable function W, where W(t) is measured in degrees Fahrenheit and t is measured in minutes. At time t =0, the temperature of the water is 55 0F. The water is heated for 30 minutes, beginning at time t = 0. Values of W (t) at selected times t for the first 20 minutes are given in the table above.
(a) Use the data in the table to estimate W'(12) . Show the computations that lead to your answer. Using correct units, interpret the meaning of your answer in the context of this problem.
(b) Use the data in the table to evaluate \(\int_{0}^{20}W'(t)dt.\) Using correct units, interpret the meaning of \(\int_{0}^{20}W'(t)dt\) in the context of this problem.
(c) For 0 ≤ t ≤ 20, the average temperature of the water in the tub is \(\frac{1}{20}\int_{0}^{20}W'(t)dt.\) Use a left Riemann sum with the four subintervals indicated by the data in the table to approximate \(\frac{1}{20}\int_{0}^{20}W'(t)dt.\) Does this approximation overestimate or underestimate the average temperature of the water over these 20 minutes? Explain your reasoning.
(d) For 20 ≤ t ≤ 25, the function W that models the water temperature has first derivative given by \(W'(t)=0.4\sqrt{t}cos (0.06t).\) Based on the model, what is the temperature of the water at time t=25 ?
▶️Answer/Explanation
Ans:
(a) \(W'(12)\approx \frac{W(15)-W(9)}{15-9}=\frac{67.9-61.8}{6}\)
= 1.017 (or 1.016)
The water temperature is increasing at a rate of approximately 1.017 F° per minute at time t = 12 minutes.
(b) \(\int_{0}^{20}W'(t)dt=W(20)-W(0)=71.0-55.0=16\)
The water has warmed by 16 F° over the interval from t = 0 to t = 20 minutes.
(c) \(\frac{1}{20}\int_{0}^{20}W(t)dt\approx \frac{1}{20}(4\cdot W(0)+5\cdot W(4)+6\cdot W(9)+5\cdot W(15))\)
\(= \frac{1}{20}(4\cdot 55.0+5\cdot 57.1+6\cdot 61.8+5\cdot 67.9)\)
\(= \frac{1}{20}\cdot 1215.8=60.79\)
This approximation is an underestimate, because a left Riemann sum is used and the function W is strictly increasing.
(d) \(W(25)=71.0+\int_{20}^{25}W'(t)dt\)
=71.0+2.043155 = 73.043