Question:
| t(hours) | 0 | 0.3 | 1.7 | 2.8 | 4 |
| \(v_P(t)\) (meters per hour) | 0 | 55 | -29 | 55 | 48 |
The velocity of a particle, P, moving along the x-axis is given by the differentiable function vp , where \(v_P(t)\) is measured in meters per hour and t is measured in hours. Selected values of \(v_P(t)\) are shown in the table above. Particle P is at the origin at time t = 0.
(a) Justify why there must be at least one time t, for 0.3 ≤ t ≤ 2.8, at which \(v_P(t)\) , the acceleration of particle P, equals 0 meters per hour per hour.
(b) Use a trapezoidal sum with the three sub-intervals [0, 0.3], [0.3, 1.7], and [1.7, 2.8] to approximate the value of \(\int_{0}^{2.8}v_{p}(t)dt.\)
(c) A second particle, Q, also moves along the x-axis so that its velocity for 0 ≤ t ≤ 4 is given by \(v_{Q}(t)=45\sqrt{t}cos(0.063t^{2})\) meters per hour. Find the time interval during which the velocity of particle Q is at least 60 meters per hour. Find the distance traveled by particle Q during the interval when the velocity of particle Q is at least 60 meters per hour.
(d) At time t = 0, particle Q is at position x = −90. Using the result from part (b) and the function vQ from part (c), approximate the distance between particles P and Q at time t = 2.8.
▶️Answer/Explanation
Ans:
(a)
\({v_{p}}'(t)=9_{p}(t)\) \(\frac{v_{p}(2.8)-v_{p}(0.3)}{2.8-0.3}\)
Since \(v_P(t)\) is a continuous and differentiable function, MVT states that there must be at least one time t, for 0.3 ≤ t ≤ 2.8 at which \({v_{p}}'(t)=\frac{v_{p}(2.8)-v_{p}(0.3)}{2.8-0.3}=\frac{55-55}{2.5}=0.\)
(b)
\(0.3\left ( \frac{55+0}{2} \right )+1.4\left ( \frac{-29+55}{2} \right )+1.1\left ( \frac{55+(-29)}{2} \right )\)
8.25 + 18.2 + 14.3
\(\int_{0}^{2.8}{v_{p}}^{(t)}=40.75\)
(c)
\(60 = 45\sqrt{t}cos (0.053t^{2})\)
t = 1.866, 3.519
1.866 ≤ t ≤ 3.519
\(\int_{1.866}^{3.519}45\sqrt{t}cos (0.063t^{2})dt\)
= 106.109
106.109 meters
(d)
\(X_p(2.8)= 40.75\)
\(x_{Q}(2.8) = -90 +\int_{0}^{2.8}45\sqrt{t}cos (0.063t^{2})dt\)
= -90 + 135.938 = 45.938
45.938 – 40.75 = 5.188
The distance between particles P and Q at t = 2.8 is 5.188 meters
Question:
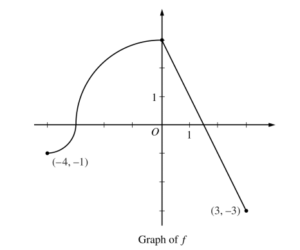
The continuous function f is defined on the interval -4 ≤ x ≤ 3. The graph of f consists of two quarter circles and one line segment, as shown in the figure above. Let \(g(x)=2x+\int_0^x f(t)dt\).
(a) Find g(-3) . Find g'(x) and evaluate g'(-3) .
(b) Determine the x-coordinate of the point at which g has an absolute maximum on the interval -4 ≤ x ≤ 3. Justify your answer.
(c) Find all values of x on the interval -4 ≤ x ≤ 3 for which the graph of g has a point of inflection. Give a reason for your answer.
(d) Find the average rate of change of f on the interval-4 ≤ x ≤ 3. There is no point c, -4 < c < 3, for which f'(c) is equal to that average rate of change. Explain why this statement does not contradict the Mean Value Theorem.
▶️Answer/Explanation
Ans:
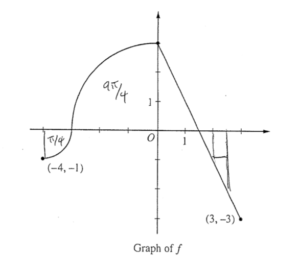
(a)
\(g(-3)=2(-3)+\int_{0}^{-3}f(t)dt = -6 -\frac{9\pi }{4}\)
\(g'(x)=\frac{d}{dx}\left ( 2x + \int_{0}^{x}f(t)dt \right )=2+f(x)\)
g'(-3) = 2 + f(-3) = 2 + 0 = 2
(b)
g'(x) = 0 2 + f(x) = 0
g'(x) f(x) = -2
x = 5/2
\(g(-4)=-8+\int_{0}^{-4}f(t)dt\)
= -8 – 2π
\(g(5/2)= 5+\int^{\frac{5}{2}}_{0} f(t)dt = + \frac{5}{4}\)
\(g(3)= 6+\int_{0}^{3}f(t)dt = 6\)
x = 5/2 , because g’ going from t to – proves it as the only relative maximum and g(5/2) is greater than g at either endpoint.
(c)
f'(x) g”(x) = d/dx (g(x)) = f'(x)
The only point of inflection for g is at x = 0, since f'(x), which is equivalent to g”, only changes signs at x = 0 on the interval -4 ≤ x ≤ 3
(d)
Avg. Rate of change = \(\frac{f(3)-f(-4)}{3-4}\)
\(\frac{-3-1}{3+4}=\frac{-2}{7}\)
Because mean value Theorem only applies when the function is continuous And differentiable on the interval, which doesn’t apply here since f(x) isn’t differentiable at x = 0.
Question:
| t (minutes) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| C (t) (ounces) | 0 | 5.3 | 8.8 | 11.2 | 12.8 | 13.8 | 14.5 |
Hot water is dripping through a coffeemaker, filling a large cup with coffee. The amount of coffee in the cup at time t, 0 ≤ t ≤ 6, is given by a differentiable function C, where t is measured in minutes. Selected values of C (t), measured in ounces, are given in the table above.
(a) Use the data in the table to approximate C'(3.5) . Show the computations that lead to your answer, and indicate units of measure.
(b) Is there a time t, 2 ≤ t ≤ 4 at which C’ (t)= 2 ? Justify your answer.
(c) Use a midpoint sum with three subintervals of equal length indicated by the data in the table to approximate the value of \(\frac{1}{6}\int_{0}^{6}C(t)dt.\) Using correct units, explain the meaning of \(\frac{1}{6}\int_{0}^{6}C(t)dt\) in the context of the problem.
(d) The amount of coffee in the cup, in ounces, is modeled by \(B(t)= 16-16e^{-0.4t}\). Using this model, find the rate at which the amount of coffee in the cup is changing when t = 5.
▶️Answer/Explanation
Ans:
(a)
\(C'(3.5)\approx \frac{\left ( (4)-(3) \right )}{4-3}=\frac{12.8-11.2}{1}=1.6\frac{08}{min}\)
(b)
Since C(t) is differentiable for all values is [2, 4], we can say that there must be some value of t in (2, 4), such as t = a, such that \(C'(a)=\frac{\left ( (4)-(2) \right )}{4-2}=\frac{12.8-8.8}{2}=2\) by the mean value theorem
so, yes’.
(c)
\(\frac{1}{6}\int_{0}^{6}C(t)dt \approx \frac{1}{6}-2.(5.3+11.2+13.8)\)
≈ 10.1 0t
This is the average value, in oz, of the amount of coffee in the cup over the interval 0 ≤ t ≤ 6.
(d)
\(B'(t)= \frac{32}{5}e^{-0.4t}\)
\(B'(5)= \frac{32}{5}e^{-2}\)
Question:
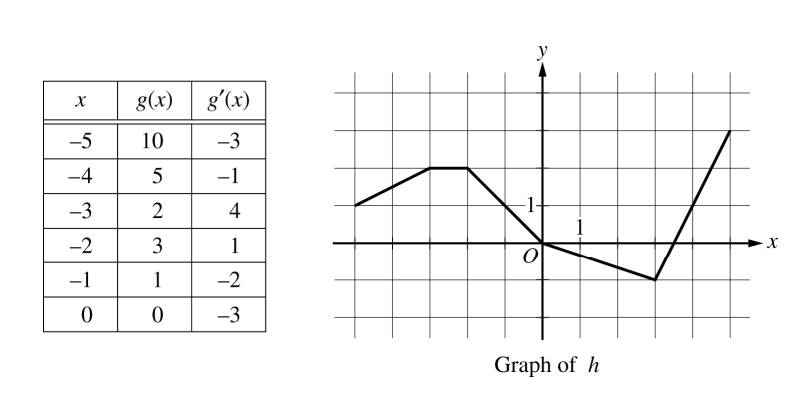
Let f be the function defined by f(x) = cos (2 x) + esin x .
Let g be a differentiable function. The table above gives values of g and its derivative g’ at selected values of x.
Let h be the function whose graph, consisting of five line segments, is shown in the figure above.
(a) Find the slope of the line tangent to the graph of f at x = π.
(b) Let k be the function defined by k(x) = h(f(x)). Find k'(π).
(c) Let m be the function defined by m(x) = g(-2x)•h(x). Find m'(2).
(d) Is there a number c in the closed interval [−5, -3 ] such that g'(c) = −4 ? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\({f}'(x) = -2sin (2x) + e^{sinx} (cos x)\)
\({f}'(π) = -2 sin (2π) + e^{sinx}(cos π)\)
\(= 0 + 1(-1)\)
\(= -1\)

(b)
\({k}'(x) = {h}'(f(x)) ({f}'(x))\)
\({k}'(π) = {h}'(f(π)){ f}'(π)\)
\(= {h}'(2) (-1)\)
\(= 1/3\)
cos (2π) + esinπ
\(1 + 1\)
(c)
In'(x) = [g'(-2x) (-2) •h(x)] + [h'(x)•g(-2x)]
In'(2) = [-2g'(-4)•h(2)] + [h'(2)•g(-4)]
=(2•-2/3) + (-1/3 •5)
\(= -4/3 + -5/3\)
\(= -9/3\)
\(= -3\)
(d)
g(x) = differentiable →g(x) continuous is mean value theorem states that
\({f}'(c)=\frac{f(b)-f(a)}{b-a}\)
\(=\frac{g(-3)-g(-5)}{-3+5}=\frac{2-10}{2}\)
\(= -8/2\)
\(= -4\)
Yes, there’s aa number C is the closed interval such that \({g}'(c) = -4\)
Question:
| t (years) | 2 | 3 | 5 | 7 | 10 |
| H(t) (meters) | 1.5 | 2 | 6 | 11 | 15 |
The height of a tree at time t is given by a twice-differentiable function H, where H (t) is measured in meters and t is measured in years. Selected values of H (t) are given in the table above.
(a) Use the data in the table to estimate H'(6). Using correct units, interpret the meaning of H'(6) in the context of the problem.
(b) Explain why there must be at least one time t, for 2 < t <10 , such that H'(t) = 2.
(c) Use a trapezoidal sum with the four subintervals indicated by the data in the table to approximate the average height of the tree over the time interval 2 ≤ t ≤ 10 .
(d) The height of the tree, in meters, can also be modeled by the function G, given by \(G(x)=\frac{100x}{1+x}\) , where x is the diameter of the base of the tree, in meters. When the tree is 50 meters tall, the diameter of the base of the tree is increasing at a rate of 0.03 meter per year. According to this model, what is the rate of change of the height of the tree with respect to time, in meters per year, at the time when the tree is 50 meters tall?
▶️Answer/Explanation
Ans:
(a)
\(H'(6)\approx \frac{\Delta H(t)}{\Delta t}\approx \frac{H(7)-H(5)/m}{(7-5)_{y}}=\frac{(11-6)m}{(7-5)y}=\frac{5 meters}{2 years}\)
When t = 6 years, the rate of which the tree is growing is H'(6) meters per year
(b)
By the MVT, as H(t) is continuous and differentiable on t ∈ (2, 10), there must be H'(c) = 2 where 2 < c < 10 if there exists \(\frac{H(b)-H(a)}{b-a}=2\) on the interval (2, 10). \(\frac{H(5)-H(3)}{(5-3)_{years}}=\frac{6m-2m}{2years}=2 m/y\) So c exists on interval c ∈ (2, 10)
(c)
Total height : \(\frac{1}{2}\left ( 1(1.5+2)+2(2+6)+2(6+11)+3(11+15) \right )\)
Average height : \(\frac{1}{10_{y}-2_{yr}} Total ht = \frac{1}{8}\times \frac{1}{2}\left ( 3.5 + 2(8)+2(17)+3(26) \right ) meters\)
(d)
\(G(x)=\frac{100x}{1+x}\) G(x) = 50 \(\frac{dx}{dt}=0.03 m/y\)
\(G'(x)=\frac{100\frac{dx}{dt}(1+x)-\left ( \frac{dx}{dt} \right )100x}{(1+x)^{2}}\) \(\frac{100\times 0.03(2)-0.03\times 100}{4}\)
\(50 = \frac{100x}{1+x}\Rightarrow 50(1+x)=100x\) \(\frac{6-3}{4}=\frac{3}{4}m/year\)
⇒ 1 = x x = 1m
Question:
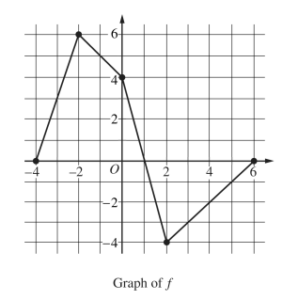
Let f be a continuous function defined on the closed interval −4 ≤ x ≤ 6. The graph of f , consisting of four line segments, is shown above. Let G be the function defined by \(G(x)=\int_{0}^{x}f(t)dt.\)
(a) On what open intervals is the graph of G concave up? Give a reason for your answer.
(b) Let P be the function defined by P (x) = G (x)• f(x). Find P'(3 ).
(c) Find \(\lim_{x\rightarrow 2}\frac{G(x)}{x^{2}-2x}.\)
(d) Find the average rate of change of G on the interval [−4, 2]. Does the Mean Value Theorem guarantee a value c, −4 < c < 2, for which G'(c) is equal to this average rate of change? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
G'(x) = f(x)
G”(x) = f'(x)
On (-4, -2) and (2, 6), G(x) is concave up because f(x) (which is equal to G'(x)) has a positive slope / is increasing.
(b)
p'(x) = G'(x) f(x) + f'(x) G(x)
p'(3) = G'(3) f(3) + f'(3) G(3)
G'(x) = f(x) \(G(3)=\int_{0}^{3}f(t)dt=-\frac{7}{2}\)
\(p'(3)=(-3)(-3)+(1)\left (- \frac{7}{2} \right )\)
(c)
\(\lim_{x\rightarrow 2}G(x)=\lim_{x\rightarrow 2}(x^{2}-2x)=0\) Must be I’hopital’s rule
\(\int_{0}^{2}f(t)dt=0\)
\(\lim_{x\rightarrow 2}\frac{G'(x)}{2x-2}=\frac{f(2)}{4-2}=\frac{-4}{2}\)
(d)
\(\int_{0}^{2}f(t)dt\) \(\int_{0}^{-4}f(t)dt= -(3+9+3+1)\)
= -16
AROC of \(G = \frac{G(2)-G(-4)}{2-(-4)}=\frac{0-(16)}{2+4}=\frac{16}{6}=\frac{8}{3}\)
The meanvalue theorem does guarantee a value of -4<c<2, for which G'(c) is equal to average rate of chang. This is because G'(x) = f(t) and x = t exists for all values, -4<x=+t<2, meaning that G(x) is continuous on the closed interval and differentiable on the open interval.