Question
The temperature, in degrees Celsius \((^{\circ}C) \), of an oven being heated is modeled by an increasing differentiable function H of time t, where t is measured in minutes. The table above gives the temperature as recorded every 4 minutes over a 16-minute period.
(a) Use the data in the table to estimate the instantaneous rate at which the temperature of the oven is changing at time t = 10. Show the computations that lead to your answer. Indicate units of measure.
(b) Write an integral expression in terms of H for the average temperature of the oven between time t =0 and time t = 16. Estimate the average temperature of the oven using a left Riemann sum with four subintervals of equal length. Show the computations that lead to your answer.
(c) Is your approximation in part (b) an underestimate or an overestimate of the average temperature? Give a reason for your answer.
▶️Answer/Explanation
(d) Are the data in the table consistent with or do they contradict the claim that the temperature of the oven is increasing at an increasing rate? Give a reason for your answer.
(a)\(H’=\frac{H(12)-H(8)}{12-8}\)=\(\frac{80-73}{4}\)=\(\frac{7}{4}^{\circ}C/min\)
(b)Average temperature is \(\frac{1}{16}H(t)dt\)
\(\int_{0}^{16}H(t)dt\simeq 4.(65+68+73+80)\)
Average temperature\( \simeq \frac{4.286}{16}=71.5^{\circ}C\)
(c) The left Riemann sum approximation is an underestimate of the integral because the graph of H is increasing. Dividing by 16 will not change the inequality, so 71.5°C is an underestimate of the average temperature.
(d) If a continuous function is increasing at an increasing rate, then the slopes of the secant lines of the graph of the function are increasing. The slopes of the secant lines for the four intervals in the table are \(\frac{3}{4}\), \(\frac{5}{4}\),\(\frac{7}{4}\)and\( \frac{10}{4}\), respectively. Since the slopes are increasing, the data are consistent with the claim. OR By the Mean Value Theorem, the slopes are also the values of \(H'(c_{k})\) for some times \(c_1 < C_2 < C_3 < C_4\), respectively. Since these derivative values are positive and increasing, the data are consistent with the claim.
Question:
| t (hours) | 0 | 1 | 3 | 6 | 8 |
| R (t) (liters / hour) | 1340 | 1190 | 950 | 740 | 700 |
Water is pumped into a tank at a rate modeled by \(W(t)= 2000e^{-t^{2}/20}\) liters per hour for 0 ≤ t ≤ 8, where t is measured in hours. Water is removed from the tank at a rate modeled by R (t) liters per hour, where R is differentiable and decreasing on 0 ≤ t ≤ 8. Selected values of R (t) are shown in the table above. At time t 0, there are 50,000 liters of water in the tank.
(a) Estimate R'(2). Show the work that leads to your answer. Indicate units of measure.
(b) Use a left Riemann sum with the four subintervals indicated by the table to estimate the total amount of water removed from the tank during the 8 hours. Is this an overestimate or an underestimate of the total amount of water removed? Give a reason for your answer.
(c) Use your answer from part (b) to find an estimate of the total amount of water in the tank, to the nearest liter, at the end of 8 hours.
(d) For 0 ≤ t ≤ 8, is there a time t when the rate at which water is pumped into the tank is the same as the rate at which water is removed from the tank? Explain why or why not.
▶️Answer/Explanation
Ans:
(a)
\(R'(2)\approx \frac{R(3)-R(1)}{3-1}=\frac{950-1190}{2}\)
R'(2) ≈ -120 L/hr2
(b)
\(\int_{0}^{8}R(t)dt\approx L_{4}=(1)(1340)+(2)(1190)+(3)(950)+(2)(740)\)
\(\int_{0}^{8}R(t)dt\approx 8,050 L\)
This is an underestimate because we are taking the left Riemann sum of a decreasing function. Therefore the left endpoints are greater than the right endpoints in each subinterval.
(c)
t = + 50, 000 L
Total left ≈ 50,000 + \(\left ( \int_{0}^{8}W(t)dt – \int_{0}^{8}R(t)dt \right )\)
\(\int_{0}^{8}W(t)dt = 7836.19532455\)
Total left ≈ 50,000 + (7836.19332455-8050)
Total left ≈ 49,786 L
(d)
T(t) = W(t) – R(t)
T(0) = 2000 – 1340 = 600 -648.47 < 0 < 600
T(8) = 81.524-700 = -618.47
When T(t) = 0, the rate of water being pumped in to the tank is equal to the rate of water being pumped out. Because the function T(t) is continuous and differentiable by IVT these exists some t on the interval [0, 8] where T(t) = 0.
Question
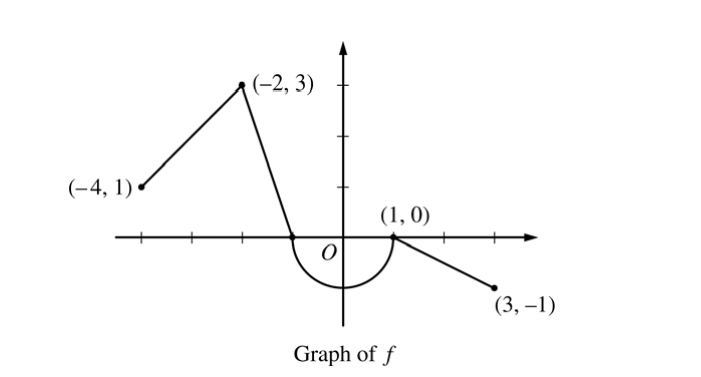
Let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. Let g be the function given by \(g(x)=\int_{1}^{x}f(t)dt.\)
(a) Find the values of g(2) and g(-2).
(b) For each of g'(-3) and g”(-3) , find the value or state that it does not exist.
(c) Find the x-coordinate of each point at which the graph of g has a horizontal tangent line. For each of these points, determine whether g has a relative minimum, relative maximum, or neither a minimum nor a maximum at the point. Justify your answers.
(d) For -4 < x < 3, find all values of x for which the graph of g has a point of inflection. Explain your reasoning.
▶️Answer/Explanation
Ans:
(a) \(g(2)=\int_{1}^{2}f(t)dt=-\frac{1}{2}(1)\left ( \frac{1}{2} \right )=-\frac{1}{4}\)
\(g(-2)=\int_{1}^{-2}f(t)dt=-\int_{-2}^{1}f(t)dt\)
\(= -\left ( \frac{3}{2}-\frac{\pi }{2} \right )=\frac{\pi }{2}-\frac{3}{2}\)
(b) \(g'(x)=f(x)\Rightarrow g'(-3)=f(-3)=2\)
\(g”(x)=f'(x)\Rightarrow g”(-3)=f'(-3)=1\)
(c) The graph of g has a horizontal tangent line where gx f'(x) = f(x) = 0. This occurs at x = −1 and x = 1.
g′(x ) changes sign from positive to negative at x = −1. Therefore, g has a relative maximum at x = −1.
g′(x) does not change sign at x = 1. Therefore, g has neither a relative maximum nor a relative minimum at x = 1.
(d) The graph of g has a point of inflection at each of x = −2, x = 0, and x = 1 because g′′(x) = f'(x) changes sign at each of these values.
Question
| t (minutes) | 0 | 4 | 9 | 15 | 20 |
| W(t) (degrees Fahrenheit) | 55.0 | 57.1 | 61.8 | 67.9 | 71.0 |
The temperature of water in a tub at time t is modeled by a strictly increasing, twice-differentiable function W, where W(t) is measured in degrees Fahrenheit and t is measured in minutes. At time t =0, the temperature of the water is 55 0F. The water is heated for 30 minutes, beginning at time t = 0. Values of W (t) at selected times t for the first 20 minutes are given in the table above.
(a) Use the data in the table to estimate W'(12) . Show the computations that lead to your answer. Using correct units, interpret the meaning of your answer in the context of this problem.
(b) Use the data in the table to evaluate \(\int_{0}^{20}W'(t)dt.\) Using correct units, interpret the meaning of \(\int_{0}^{20}W'(t)dt\) in the context of this problem.
(c) For 0 ≤ t ≤ 20, the average temperature of the water in the tub is \(\frac{1}{20}\int_{0}^{20}W'(t)dt.\) Use a left Riemann sum with the four subintervals indicated by the data in the table to approximate \(\frac{1}{20}\int_{0}^{20}W'(t)dt.\) Does this approximation overestimate or underestimate the average temperature of the water over these 20 minutes? Explain your reasoning.
(d) For 20 ≤ t ≤ 25, the function W that models the water temperature has first derivative given by \(W'(t)=0.4\sqrt{t}cos (0.06t).\) Based on the model, what is the temperature of the water at time t=25 ?
▶️Answer/Explanation
Ans:
(a) \(W'(12)\approx \frac{W(15)-W(9)}{15-9}=\frac{67.9-61.8}{6}\)
= 1.017 (or 1.016)
The water temperature is increasing at a rate of approximately 1.017 F° per minute at time t = 12 minutes.
(b) \(\int_{0}^{20}W'(t)dt=W(20)-W(0)=71.0-55.0=16\)
The water has warmed by 16 F° over the interval from t = 0 to t = 20 minutes.
(c) \(\frac{1}{20}\int_{0}^{20}W(t)dt\approx \frac{1}{20}(4\cdot W(0)+5\cdot W(4)+6\cdot W(9)+5\cdot W(15))\)
\(= \frac{1}{20}(4\cdot 55.0+5\cdot 57.1+6\cdot 61.8+5\cdot 67.9)\)
\(= \frac{1}{20}\cdot 1215.8=60.79\)
This approximation is an underestimate, because a left Riemann sum is used and the function W is strictly increasing.
(d) \(W(25)=71.0+\int_{20}^{25}W'(t)dt\)
=71.0+2.043155 = 73.043
Question
| t (minutes) | 0 | 2 | 5 | 9 | 10 |
| H(t) (degrees Celsius) | 66 | 60 | 52 | 44 | 43 |
As a pot of tea cools, the temperature of the tea is modeled by a differentiable function H for 0 ≤ t ≤ 10, where time t is measured in minutes and temperature H(t) is measured in degrees Celsius. Values of H(t) at selected values of time t are shown in the table above.
(a) Use the data in the table to approximate the rate at which the temperature of the tea is changing at time t = 3.5. Show the computations that lead to your answer.
(b) Using correct units, explain the meaning of \(\frac{1}{10}\int_{0}^{10}H(t)dt\) in the context of this problem. Use a trapezoidal sum with the four subintervals indicated by the table to estimate \(\frac{1}{10}\int_{0}^{10}H(t)dt.\)
(c) Evaluate \(\int_{0}^{10}H'(t)dt.\) Using correct units, explain the meaning of the expression in the context of this problem.
(d) At time t = 0, biscuits with temperature 100 0C were removed from an oven. The temperature of the biscuits at time t is modeled by a differentiable function B for which it is known that
B'(t) = – 13.84e-0.173t . Using the given models, at time t = 10, how much cooler are the biscuits than the tea?
▶️Answer/Explanation
Ans:
(a)
\(\frac{H(5)-H(2)}{5-2}=\frac{-8}{3}\frac{0_{C}}{min}\)
(b)
\(\frac{1}{10}\int_{0}^{10}H(t)dt\approx \frac{\left [2(\frac{66+180}{2}) +3(\frac{52+60}{2})+4(\frac{44+52}{2})+1(\frac{43+44}{2}) \right ]}{10}=52.95\)
This represents the average temperature in degree Celsius of the tea over the interval 0 ≤ t ≤ 10
(c)
\(\int_{0}^{10}H'(t)dt= H(10)-H(0)=43-66=-23^{0}C\)
This expression shows the total change in temperature in degree Celsius from t = 0 to t = 10.
(d)
\(B'(t)=-13.84e^{-.173t}\)
\(B(10)=\int_{0}^{10}-13.84e^{-.173t}+100 = 100-65.817 = 34.1827\)
43-341827 = 8.817
= 88170C Celsius
