Question:
The function f is defined by \(f(x)=\sqrt{25-x^{2}}\) for -5 ≤ x ≤ 5.
(a) Find f'(x).
(b) Write an equation for the line tangent to the graph of f at x = -3.
(c) Let g be the function defined by \(g(x)=\left\{\begin{matrix}
f(x) &for -5\leq x\leq -3 & & \\x+7
&for -3<x\leq 5. & &
\end{matrix}\right.\)
Is g continuous at x = -3 ? Use the definition of continuity to explain your answer
(d) Find the value of \(\int_{0}^{5}x\sqrt{25-x^{2}}dx.\)
▶️Answer/Explanation
Ans:
(a)
\(= (25-x^{2})^{1/2}\)
\(f'(x)=\frac{1.-2x}{2\sqrt{25-x^{2}}}=\frac{-x}{\sqrt{25-x^{2}}}\)
(b)
\(f'(-3)=\frac{3}{\sqrt{25-9}}=\frac{3}{\sqrt{16}}=\frac{3}{4}\) \(f(-3)=\sqrt{25-9}= \sqrt{16}=4\)
\(y = \frac{3}{4}(x+3)+4\)
(c)
\(\lim_{x\rightarrow -3^{-}}g(x)=f(-3)=4\) therefore \(\lim_{x\rightarrow -3}g(x)=4\)
\(\lim_{x\rightarrow -3^{+}}g(x)=-3+7=4\)
g(-3) = f(-3) = 4 \(\lim_{x\rightarrow -3}g(x)\) exists and is equal to g(-3)
g is continuous at x = -3
(d)
u = 25-x2 \(\frac{-1}{2}\int_{25}^{0}4^{1/2}du = \frac{1}{2}\int_{0}^{25}4^{1/2}du = \frac{1}{2}.\frac{24}{3}^{3/2}\int_{0}^{25}\)
\(\frac{-1}{2}du = +2xdx\)
\(= \frac{1}{3}.25^{3/2}=\frac{125}{3}\)
Question:
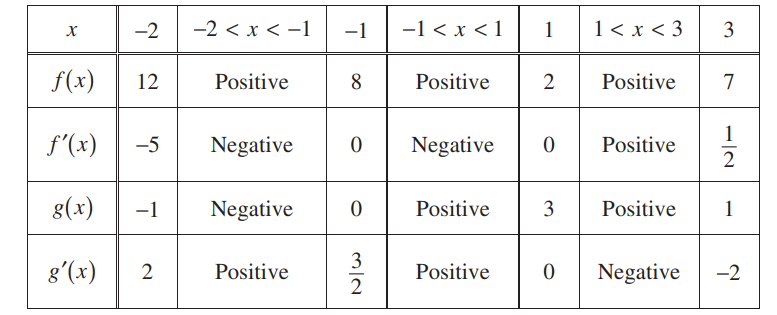
The twice-differentiable functions f and g are defined for all real numbers x. Values of f, f’, g, and g’ for various values of x are given in the table above.
(a) Find the x-coordinate of each relative minimum of f on the interval [-2, 3] . Justify your answers.
(b) Explain why there must be a value c, for -1 < c < 1, such that f”(c) =0.
(c) The function h is defined by h(x) = In (f(x)). Find h'(3). Show the computations that lead to your answer.
(d) Evaluate \(\int_{-2}^{3}f'(g(x))g'(x)dx.\)
▶️Answer/Explanation
Ans:
(a)
Critical numbers : x = -1, 1
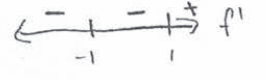
f has a rel. min. at x = 1 because f'(1) = 0 and f’ switches sign from negative to positive there.
(b)
f'(-1) = 0 and f'(1) = 0, and f'(x) is differentiable and continuous on the internal so by rolle’s Theorem there is some value c where f”(c) = 0.
(c)
\(h'(x)=\frac{f'(x)}{f(x)}\)
\(h'(3)=\frac{f'(3)}{f(3)}\)
\(h'(3)=\frac{\frac{1}{0}}{7}\)
\(h'(3)=\frac{1}{2}\cdot \frac{1}{7}\)
\(h'(3)=\frac{1}{14}\)
(d)
u = g(x)
du = g'(x) dx
\(\int f'(u)du\)
\(\left [ f\left ( g(x) \right ) \right ]_{-2}^{3}\)
\(f(g(3)) – f(g(-2))\)
\(f(1) – f(-1)\)
\(2-8\)
\(-6\)