Question
At t = 0 a particle starts at rest and moves along a line in such a way that at time t its acceleration is \(24t^{2}\) feet per second per second. Through how many feet does the particle move during the first 2 seconds?
(A) 32 (B) 48 (C) 64 (D) 96 (E) 192
▶️Answer/Explanation
Ans:A
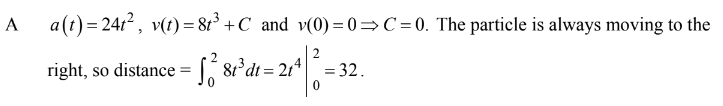
Question
The acceleration α of a body moving in a straight line is given in terms of time t by α= −8 6t . If the velocity of the body is 25 at t =1 and if s (t) is the distance of the body from the origin at time t, what is s(4)-s(2)?
(A) 20 (B) 24 (C) 28 (D) 32 (E) 42
▶️Answer/Explanation
Ans:D
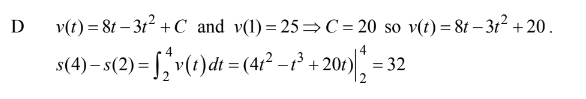
Question
The velocity of a particle moving on a line at time t is \(v=3t^{\frac{1}{2}}+5t^{\frac{3}{2}}\) meters per second. How many meters did the particle travel from t = 0 to t = 4?
(A) 32 (B) 40 (C) 64 (D) 80 (E) 184
▶️Answer/Explanation
Ans:D
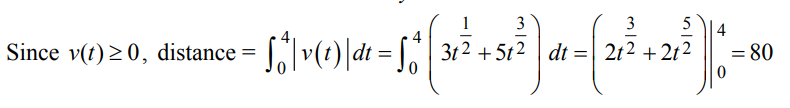
Question
What is the domain of the function f given by\(f(x)=\frac{\sqrt{x^{2}-4}}{x-3}\)?
(A) {x : x ≠3 } (B) {x :|x| ≤ 2} (C) {x :|x| ≥ 2} (D) {x : |x| ≥ 2 and x ≠3 } (E) {x: x ≥ 2 and x≠ 3}
▶️Answer/Explanation
Ans:D
\(x^2-4\geq 0 and x\neq 3\Rightarrow |x|\geq 2 and x\neq 3\)
