Question:
A company designs spinning toys using the family of functions \(y = cx\sqrt{4-x^{2}},\) where c is a positive constant. The figure above shows the region in the first quadrant bounded by the x-axis and the graph of \(y = cx\sqrt{4-x^{2}},\) for some c. Each spinning toy is in the shape of the solid generated when such a region is revolved about the x-axis. Both x and y are measured in inches.
(a) Find the area of the region in the first quadrant bounded by the x-axis and the graph of \(y = cx\sqrt{4-x^{2}},\) for c = 6.
(b) It is known that, for \(y = cx\sqrt{4-x^{2}},\frac{dy}{dx}=\frac{c\left ( 4-2x^{2} \right )}{\sqrt{4-x^{2}}}.\) For a particular spinning toy, the radius of the largest cross-sectional circular slice is 1.2 inches. What is the value of c for this spinning toy?
(c) For another spinning toy, the volume is 2π cubic inches. What is the value of c for this spinning toy?
▶️Answer/Explanation
Ans:
(a)
\(y = 6\times \sqrt{4-x^{2}}=0\)
x = 0, x = 2
\(A = \int_{0}^{2}6\times \sqrt{4-x^{2}}dx\) u = 4-x2
du = -2xdx
\(A = \int_{4}^{0}-3 \sqrt{u}du=3\int_{0}^{4}u^{\frac{1}{2}}du=3 u^{3/2}\cdot \frac{2}{3}|_{0}^{4}\)
A = 2(43/2 – 03/2) = 2(22.3/2 – 0) = 2(8) = 16
A = 16
(b)
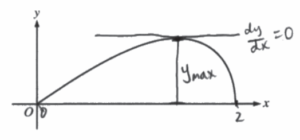
Largest cross section where y is greatest (maximum of y on graph).
Find max:
\(\frac{dy}{dx}=\frac{c(4-2x^{2})}{\sqrt{4-x^{2}}}=0 \rightarrow c(4-2x^{2})=0\)
4 = 2x2
\(x = \sqrt{2}\)
At \(x = \sqrt{2}\), y = 1.2 (largest radius of cross-section equals 1.2, which is max y value)
\(y = cx\sqrt{4-x^{2}}\)
\(1.2 = c\sqrt{2}\left ( \sqrt{4-(\sqrt{2})^{2}} \right )=c\sqrt{2}\left ( \sqrt{4-2} \right )=c\sqrt{2}(\sqrt{2})=2c\)
c = 1.2/2 = 0.6 → c = 0.6
(c)
\(v = \pi \int_{0}^{2}y^{2}dx=\pi \int_{0}^{2}(cx\sqrt{4-x^{2}})^{2}dx = \pi c^{2}\int_{0}^{2}x^{2}(4-x^{2})dx=\pi c^{2}\int_{0}^{2}(4x^{2}-x^{4})dx\)
\(v = \pi c^{2}\left [ \frac{4x^{3}}{3}-\frac{x^{5}}{5}|_{0}^{2} \right ]= \pi c^{2}\left [ \left ( \frac{4(8)}{3}-\frac{32}{5} \right )-(0-0) \right ]\)
\(v = \pi c^{2}\left ( \frac{32(5)}{3(5)}-\frac{32(3)}{5(3)} \right )= \pi c^{2}\left ( \frac{2(32)}{15} \right )== \pi c^{2}\left ( \frac{64}{15} \right )\)
\(2\pi =\pi c^{2}\left ( \frac{64}{15} \right )\)
\(c^{2}=\frac{30}{64}\rightarrow c= \sqrt{\frac{30}{64}}=\frac{\sqrt{30}}{8}\)
