Question
The area of the region enclosed by the graph of \(y=x^2+1\)and the line y = 5 is
(A) \(\frac{14}{3}\) (B) \(\frac{16}{3}\) (C) \(\frac{28}{3}\) (D) \(\frac{32}{3}\) (E) 8π
▶️Answer/Explanation
Ans:D
The area of the region is given by\(\int_{-2}^{2}(5-(x^2+1))dx=2(4x-\frac{1}{3}x^3)|_{0}^{2}=2\left ( 8-\frac{8}{3} \right )=\frac{32}{3}\)
Question
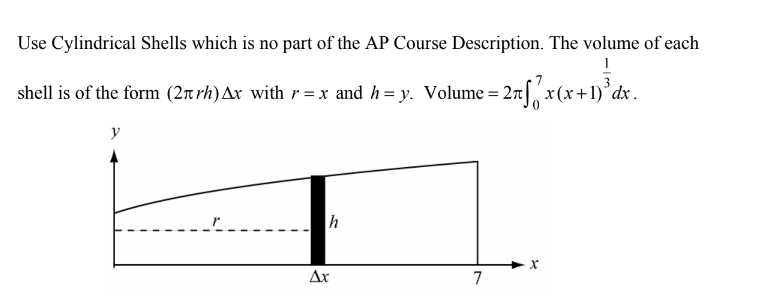
Let R be the region in the first quadrant enclosed by the graph of \( y=(x+1)^{\frac{1}{3}}dx\) , the line x = 7 ,the x-axis, and the y-axis. The volume of the solid generated when R is revolved about the y-axis is given by
(A)\(\pi \int_{0}^{7}(x+1)^{\frac{2}{3}dx}\) (B)\(2\pi \int_{0}^{7}x(x+1)^{\frac{1}{3}dx}\) (C)\(\pi \int_{0}^{2}(x+1)^{\frac{2}{3}dx}\) (D)\(2\pi \int_{0}^{2}x(x+1)^{\frac{1}{3}dx}\) (E)\(\pi \int_{0}^{7}(y^{3}-1)^{2}dy\)
▶️Answer/Explanation
Ans:B
Question
If\( y = 2x – 8\) , what is the minimum value of the product xy ?
(A) –16 (B) –8 (C) –4 (D) 0 (E) 2
▶️Answer/Explanation
Ans:B
\(p(x)=2x^2-8x;P'(x)=4x-8;p\)’; changes from negative to positive at x= 2.p (2)= 8
Question
The area of the region between the graph of \(y= 4x^3 +2\) and the x-axis from \(x =1\) to \(x = 2\) is
(A) 36 (B) 23 (C) 20 (D) 17 (E) 9
▶️Answer/Explanation
Ans:D
\(\int_{0}^{2}(4x^3+2)dx= (x^4+2x)|_{0}^{2}=(16+4)-(1+2)=17\)
