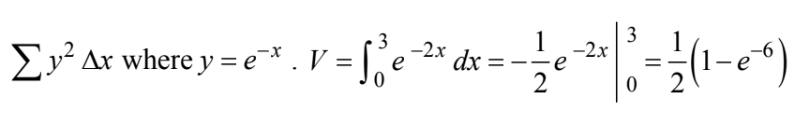Question
The base of a solid is the region in the first quadrant bounded by the y-axis, the x-axis, the graph of \(y=e^{x}\) and the vertical line x=1. For this solid, each cross section perpendicular to the x
x-axis is a square. What is the volume of the solid?
A e-1
B \(\frac{1}{2}e^{2}-1\)
C \(e^{2}-1\)
D \(2e^{2}-2\)
▶️Answer/Explanation
Ans:B
The area of a square of side length s is \(s^{2}\). A typical cross section of the solid is a square with side from the x -axis to the graph of \(y=e^{x}\). The length of the side of the square is therefore \(s=e^{x}\), so the area of the square is \((e^{x})^{2}=e^{2x}\). The volume of the solid is found using the definite integral of the cross-sectional area.
\(\int ^{1}_{0}e^{2x}dx=\frac{1}{2}e^{2x}|^{1}_{0}=\frac{1}{2}e^{2}-\frac{1}{2}\)
Question
The base of a solid is the region enclosed by the graph of \(y=e^{-x}\) , the coordinate axes, and the line x = 3. If all plane cross sections perpendicular to the x-axis are squares, then its volume is
(A)\(\frac{\left ( 1-e^{-6} \right )}{2}\)
(B)\(\frac{1}{2}e^{-6}\)
(C)\(e^{-6}\)
(D)\(e^{-3}\)
(E)\(1-e^{-3}\)
▶️Answer/Explanation
Ans:A
Question
The base of a solid is the region in the first quadrant enclosed by the parabola\( y = 4x^{3}\), the line x =1, and the x-axis. Each plane section of the solid perpendicular to the x-axis is a square. The volume of the solid is
(A) \(\frac{4π}{3}\) (B) \(\frac{16π}{5}\) (C) \(\frac{4}{3}\) (D) \(\frac{16}{5}\) (E)\(\frac{64}{5}\)
▶️Answer/Explanation
Ans:D
Square cross – sections :\(\sum y^2\Delta x\) where \(y=4x^2\).
Volume\( =\int_{0}^{1}16x^4dx =\left | \frac{16}{5}x^4 \right |_0^1= \frac{16}{5}\)
Question
The base of a solid is the region enclosed by the graph of \(y=e^{-x}\) , the coordinate axes, and the line
x = 3. If all plane cross sections perpendicular to the x-axis are squares, then its volume is
(A)\(\frac{\left ( 1-e^{-6} \right )}{2}\)
(B)\(\frac{1}{2}e^{-6}\)
(C)\(e^{-6}\)
(D)\(e^{-3}\)
(E)\(1-e^{-3}\)
▶️Answer/Explanation
Ans:A
Square cross sections: