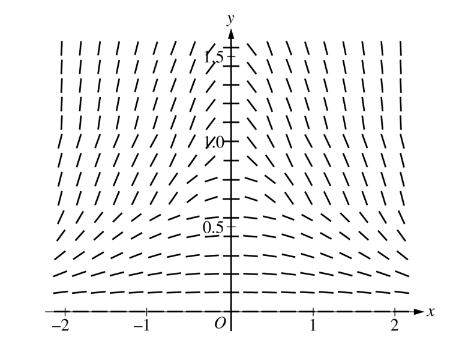
Question
The slope field for a certain differential equation is shown above. Which of the following could be a solution to the differential equation with the initial condition y( 0) =1?
(A) y= cosx
(B)\(y= 1-x^{2}\)
(C)\(y=e^{x}\)
(D)\(y=\sqrt{1-x^{2}}\)
(E)\(y=\frac{1}{1+x^{2}}\)
▶️Answer/Explanation
Ans:E
Question
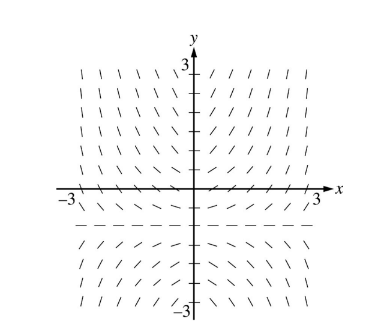
Shown above is a slope field for which of the following differential equations?
(A) \(\frac{dy}{dx}\)=xy+x
(B) \(\frac{dy}{dx}\)=xy+y
(C) \(\frac{dy}{dx}\)=y+1
(D) \(\frac{dy}{dx}\)=\((x+1)^{2}\)
▶️Answer/Explanation
Ans:A
Question
The figure below shows a slope field for one of the differential equations given below. Identify the equation.
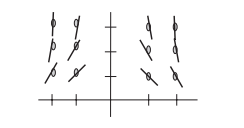
(A) \(\frac{\mathrm{d} y}{\mathrm{d} x}=y-x\)
(B) \(\frac{\mathrm{d} y}{\mathrm{d} x}=-xy\)
(C) \(\frac{\mathrm{d} y}{\mathrm{d} x}=2x\)
(D) \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{x}{y}\)
▶️Answer/Explanation
Ans:(B)
By observing different properties of the slope field, we can eliminate the answer choices. Notice that in the column x = 0, the slope is constantly 0. So when x = 0, the slope is independent of the changing y-value in that column. This eliminates the choices (A) \(\frac{\mathrm{d} y}{\mathrm{d} x}=y-x\) and (E)\(\frac{\mathrm{d} y}{\mathrm{d} x}=-2y\)
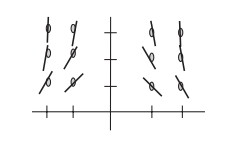
Now notice that when x and y are positive, the slope in the graph is negative. This eliminates choices (C) and (D). The correct answer is (B) \(\frac{\mathrm{d} y}{\mathrm{d} x}=-xy\)