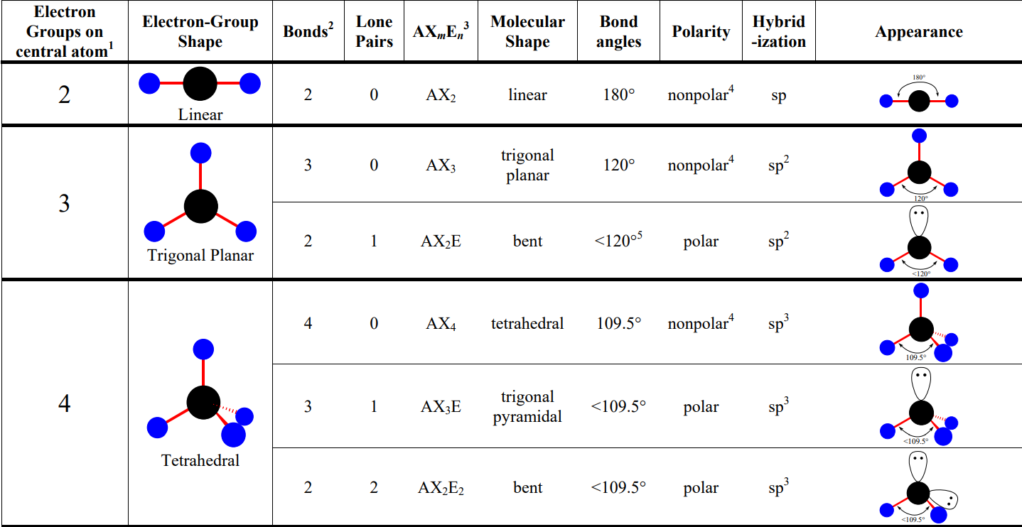
VSEPR Model
- VSEPR Model: Valence shell electron-pair repulsion → used to predict the geometries of covalent compound
- States that structure of a molecule is principally determined by minimizing electron-pair repulsions between atoms
- The lone and bonded pairs around an atom will be positioned as far apart as possible to minimize repulsion
- States that structure of a molecule is principally determined by minimizing electron-pair repulsions between atoms
- The number of pairs determines:
- Bond angles
- Underlying structure
- Polarity
- The number of atoms determines: actual shape
- Things to know
- Lone pairs take up more space than bonded (shared pairs) .
- So replacing bonded pairs with squeezes bonding pairs together and causes bond angles to become slightly less
- Multiple bonds count as one shared pair (electron domain/steric number)
- Lone pairs take up more space than bonded (shared pairs) .
- Note: sp hybridized & sp2 hybridized = flat→ atoms bonded are in the same plane; every other electron group shape = not flat → atoms bonded must exist in a diff plane
- Electron Geometry: determines shape; count bonds (shared pairs) and lone pairs
- Molecular Geometry: what you see; count only bonds
Hybridization
Hybridization and the Localized Electron Model
- Hybridization: mixing of the atomic orbitals to form special orbitals for bonding
- Reason: orbitals blend bcuz leads to minimal energy for the molecule and suitable geometry
- Atomic orbitals (e.g s, p, d, f) are only present in single, unbonded atoms
- When atoms form bonds, their atomic orbitals form hybrid orbitals
- Model summarized: an atom in a molecule might adopt a different set of atomic orbitals (called hybrid orbitals) from those it has in the free state
- Makes sense: bcuz assumes that the individual atoms respond as needed to achieve the minimum energy for the molecule
- The electrons will be arranged to give each atom a noble gas configuration, where possible, and to minimize electron-pair repulsions.
- Makes sense: bcuz assumes that the individual atoms respond as needed to achieve the minimum energy for the molecule
Sp3 Hybridization
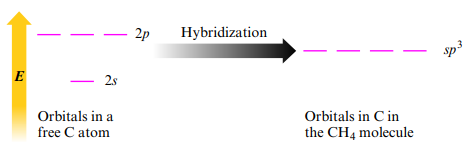
- Can say that the central atom undergoes sp3 hybridization or is sp3 hybridized
- Tetrahedral electron geometry = Sp3 hybridization
- Formed from 1 s and 3 p orbitals:
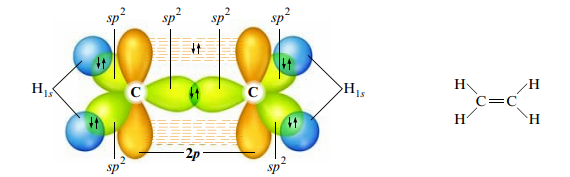
Sp2 Hybridization
- Trigonal planar arrangement (three effective pairs) of atomic orbitals → sp2
- The plane of the sp2 hybridized orbitals is determined by which p orbitals are used
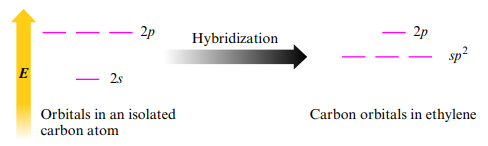
- The three sp2 orbitals on each carbon can be used to share electrons
Sp Hybridization
- Linear geometry (2 effective pairs) = sp hybridization
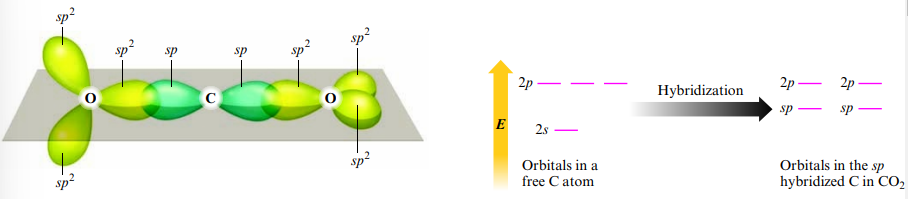
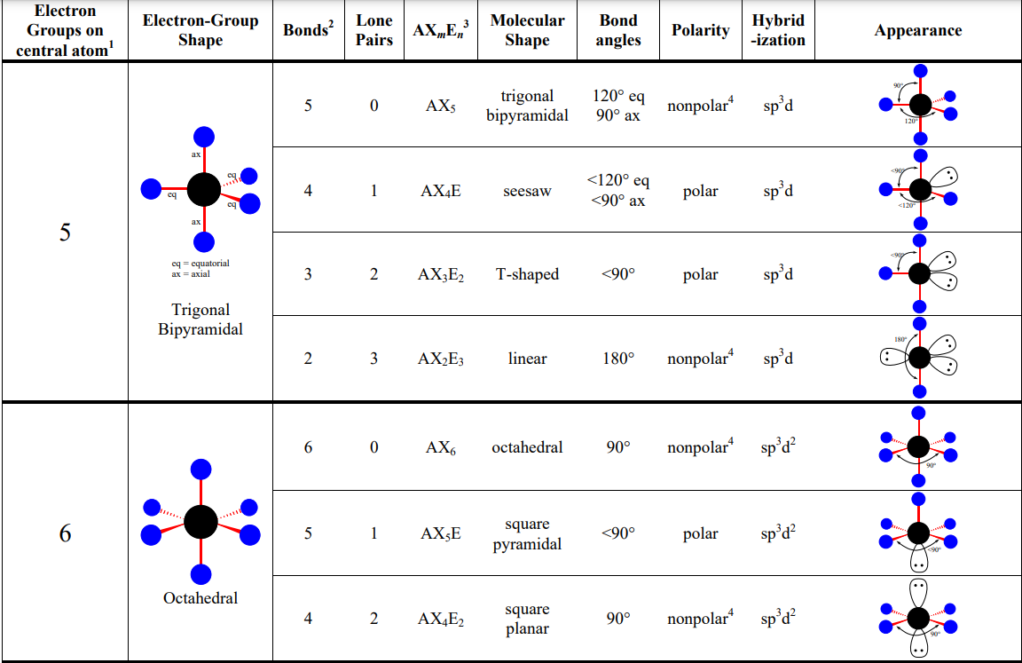
Dsp3 Hybridization
- Trigonal bipyramidal arrangement (five effective pairs) around atom imply dsp3 hybridization
- Note: AP exam won’t ask about hybridization for domains 5 and 6
D2sp3 Hybridization
- Octahedral arrangement (six electron pairs) around an atom imply d2sp3 hybridization of the atom.
Sigma vs Pi Bonds
- Sigma bond: bond formed from overlapping linear hybridized orbitals
- Bonds are formed from electron pairs shared in an area centered on the line running between the atoms (internuclear axis)
- Can be described as being localized (doesn’t move around) → electrons stay put between the 2 atoms
- Pi bond: formed from overlapping unhybridized and parallel p orbitals
- Result from atoms sharing an electron pair in the space above and below the internuclear axis/sigma bond; causes atoms to be in the same plane
- Only appear in a multiple bond
- Double bond = one sigma + one pi
- Triple bond = one sigma + 2 pi
- In situation where resonance exists: there is a pair of [delocalized] electrons (pi bond) resonating between two locations
Hybridization Trick
- H = ½ (V + M – C + A)
- V = # of valence electrons
- M = # of monovalent atoms bonded
- Monovalent = valency of one
- C = cationic charge
- A = Anionic charge
- With compounds with more than one central atom, to find H of single atom, divide value by number of atoms
