Question
A student has 100. mL of 0.400 M \(CuSO_4(aq)\) and is asked to make 100. mL of 0.150 M \(CuSO_4\)(aq) for a spectrophotometry experiment. The following laboratory equipment is available for preparing the solution: centigram balance, weighing paper, funnel, 10 mL beaker, 150 mL beaker, 50 mL graduated cylinder, 100 mL volumetric flask, 50 mL buret, and distilled water.
(a) Calculate the volume of 0.400 M\( CuSO_4\)(aq) required for the preparation.
(b) Briefly describe the essential steps to most accurately prepare the 0.150 M \(CuSO_4\)(aq) from the 0.400 M \(CuSO_4\)(aq) using the equipment listed above. The student plans to conduct a spectrophotometric analysis to determine the concentration of \(Cu^{2+}\)(aq) in a solution. The solution has a small amount of \(Co(NO_3)_2\)(aq) present as a contaminant. The student is given the diagram below, which shows the absorbance curves for aqueous solutions of \(Co^{2+}\)(aq) and\( Cu^{2+}\)(aq).
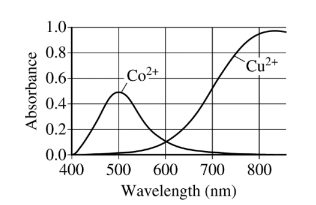
(c) The spectrophotometer available to the student has a wavelength range of 400 nm to 700 nm. What wavelength should the student use to minimize the interference from the presence of the \(Co^{2+}\)(aq) ions?
▶️Answer/Explanation
(a) \(M_1V_{1}=M_{2}V_{2}\)
\(V_{2}=\frac{(0.150M)(0.100L)}{0.400M}\)
\(V_{2}=0.0375L \times \frac{1000mL}{1L}=37.5mL\)
(b) Use the buret to dispense 37.5 mL of\( CuSO_4\) solution into the volumetric flask. Fill to the mark with distilled water.
(c) 700 nm (Any wavelength from 650 to 700 nm is acceptable.)
Question
A student is given the task of determining the molar concentration of a CuSO4 solution using two different procedures, precipitation and spectrophotometry.
For the precipitation experiment, the student adds 20.0 mL of 0.200 M Ba(NO3)2 to 50.0 mL of the CuSO4 (aq). The reaction goes to completion, and a white precipitate forms. The student filters the precipitate and dries it overnight. The data are given in the following table.

(a) Write a balanced net ionic equation for the precipitation reaction.
(b) Calculate the number of moles of precipitate formed.
(c) Calculate the molarity of the original CuSO4 solution.
For the spectrophotometry experiment, the student first makes a standard curve. The student uses a 0.1000 M solution of CuSO4 (aq) to make three more solutions of known concentration (0.0500 M, 0.0300 M, and 0.0100 M) in 50.00 mL volumetric flasks.
(d) Calculate the volume of 0.1000 M CuSO4(aq) needed to make 50.00 mL of 0.0500 M CuSO4(aq)
(e) Briefly describe the procedure the student should follow to make 50.00 mL of 0.0500 M CuSO4(aq) using 0.1000 M CuSO4 (aq), a 50.00 mL volumetric flask, and other standard laboratory equipment. Assume that all appropriate safety precautions will be taken.
The standard curve is given below.
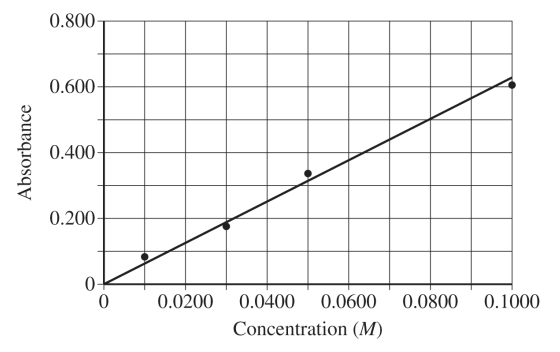
(f) The absorbance of the CuSO4 solution of unknown concentration is 0.219. Determine the molarity of the solution.
(g) A second student performs the same experiment. There are a few drops of water in the cuvette before the second student adds the CuSO4 (aq) solution of unknown concentration. Will this result in a CuSO4 (aq) concentration for the unknown that is greater than, less than, or equal to the concentration determined in part (f) ? Justify your answer.
▶️Answer/Explanation
Ans:
(a) For the correct balanced equation (state symbols not required):
Ba2+ (aq) + SO42- (aq) →BaSO4(s)
(b) For the correct calculated value of the mass of precipitate (may be implicit):
1.136 g – 0.764 g = 0.372 g BaSO4
For the correct calculated value of the number of moles, consistent with mass of precipitate:
\(0.372 g \times \frac{1 mol}{233.39 g}= 0.00159 mol\)
(c) For the correct calculated value, consistent with part (b):
0.00159 mol BaSO4 × \(\frac{1 mol CuSO_{4}}{1 mol BaSO_{4}}\) = 0.00159 mol CuSO4
\(\frac{0.00159 mol CuSO_{4}}{0.0500 L}\)= 0.0318 M CuSO4 (0.0319 M if decimals are carried)
(d) For the correct calculated value:
M1V1 = M2V2
\(V_{1}= \frac{(0.0500 M)(50.00 mL)}{(0.1000 M)}=25.0 mL\)
(e) For a correct technique to measure the volume of solution:
First, measure out the correct volume of 0.1000 M CuSO4 solution with a 25.0 mL volumetric pipet (graduated cylinder or buret is acceptable).
For a correct technique to dilute the solution to the final volume:
Transfer the 25.0 mL of solution to a 50.00 mL volumetric flask and dilute the solution with water up to the 50.00 mL mark.
(f) For the correct value (between 0.032 M and 0.038 M):
Accept one of the following:
• \(y = mx = \frac{0.63}{0.1000}x=6.3x\)
\(x = \frac{y}{6.3}=\frac{0.219 M}{6.3}=0.035 M\)
• Estimated value from the graph within the specified range.
(g) For the correct answer:
The concentration will be less than that determined in part (f).
For a valid justification:
The additional water will decrease the concentration of CuSO4 in the cuvette. Therefore, there will be a decrease in absorbance (according to the Beer-Lambert law). This dilution
results in a lower estimated concentration of CuSO4.
