Question
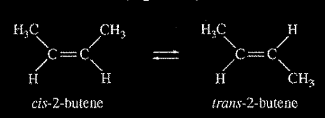
The half-life (1/2) of the catalyzed isomerization of cis-2-butene gas to produce trans-2-butene gas, represented above, was measured under various conditions, as shown in the table below.

(a) The reaction is first order. Explain how the data in the table are consistent with a first-order reaction.
(b) Calculate the rate constant, k, for the reaction at 350. K. Include appropriate units with your answer.
(c) Is the initial rate of the reaction in trial I greater than, less than, or equal to the initial rate in trial 2? Justify your answer.
(d) The half-life of the reaction in trial 4 is less than the half-life in trial 1. Explain why, in terms of activation energy.
▶️Answer/Explanation
(a) For a first-order reaction, the half-life is independent of reactant concentration (or pressure) at constant 7, as shown in trials 1, 2, and 3.
(b) \(k=\frac{0.693}{t_{1/2}}=\frac{ 0.693}{ 100 s} = 0.00693 s^{-1}\)
(c) The initial rate in trial I is less than that in trial 2 because rate = k[cis-2-butene] or rate \(= k _{Pcis-2-butene}\) (with reference to values from both trials). OR because the initial concentration of cis-2-butene in trial 1 is less than that in trial 2 and it is constant.
(d) The temperature is higher in trial 4, meaning that the \(KE_{avg}\) of the molecules is greater. Consequently, in this trial a greater fraction of collisions have sufficient energy to overcome the activation energy barrier, thus the rate is greater.
Question
\(2 NO(g) + Br_2(g) \rightarrow 2 NOBr(g)\)
A rate study of the reaction represented above was conducted at 25°C. The data that were obtained are shown in
the table below.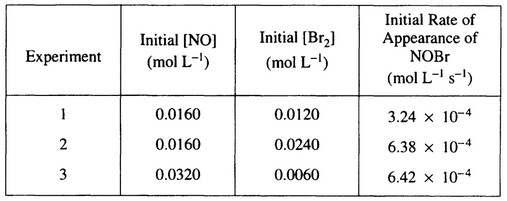
(a) Calculate the initial rate of disappearance of \(Br_2(g)\) in experiment
(b) Determine the order of the reaction with respect to each reactant, \(Br_2(g)\) and NO(g). In explain your reasoning.
(c) For the reaction,
(i) write the rate law that is consistent with the data, and
(ii) calculate the value of the specific rate constant, k, and specify units.
(d) The following mechanism was proposed for the reaction:
\(Br_2(g) + NO(g) \rightarrow NOBr_2(g)\) slow
\(NOBr_2(g) + NO(g) \rightarrow 2 NOBr(g)\) fast
Is this mechanism consistent with the given experimental observations? Justifv vour answer.
▶️Answer/Explanation
Answer:
(a) Rate of \(Br_2(g)\) loss occurs at 1/2 the rate of NOBr(g) formation.
Rate of \(Br_2(g)\) loss = \(\frac{3.24 \times 10^{-4} M}{2 sec}=1.62 \times 10^{-4} M sec^{-1} (or mol L^{-1 }sec^{-1})\)
(b) Comparing experiments 1 and 2, [NO] remains constant, \([Br]_2\) doubles, and rate doubles;
therefore, rate ∝ \([Br_2]^1 \Rightarrow \) reaction is first-order with respect to \([Br_2]\).
\(\frac{6.38 \times 10^{-4}}{6.42 \times 10^{-4}} ≅ 1 = \frac{k[NO]^x[Br_2]}{k[NO]^x[Br_2]}=\frac{k[0.0160]^x[0.0240]}{k[0.0320]^x[0.0060]}=(\frac{1}{2})^x4 = 1 \Rightarrow\)
\(\frac{1}{4}=(\frac{1}{2})^x \Rightarrow x = 2 \Rightarrow \) reaction is second-order with respect to [NO]
(c) (i) Rate = \(k[NO]^2[Br_2]\)
(ii) \(k=\frac{Rate}{[NO]^2[Br_2]}=\frac{3.24 \tiems 10^{-4} M sec^{-1}}{(0.0160)^2(0.0120)M^3}=105 M^{-2} sec^{-1} (or 105 L^2 mol^{-2} sec^{-1)\)
(Using rate of \(Br_2(g)\) loss = 1.62 \times 10^{-4} M sec^{-1} \Rightarrow k = 52.7 M^{-2} sec^{-1}\) is also correct).
(d) No, it is not consistent with the given experimental observations.
This mechanism gives a reaction that is first-order in [NO], and first-order in \([Br_2]\), as those are the two reactants in the rate-determining step. Kinetic data show the reaction is second-order in [NO] (and first-order in \([Br_2])\), so this cannot be the mechanism.
Question
Nitrogen dioxide, \(NO_2\)(g), is produced as a by-product of the combustion of fossil fuels in internal combustion engines. At elevated temperatures NO2(g) decomposes according to the equation below.
\(2 NO_2(g) → 2 NO(g) + O_2\)(g)
The concentration of a sample of \(NO_2\(g) is monitored as it decomposes and is recorded on the graph directly below. The two graphs that follow it are derived from the original data
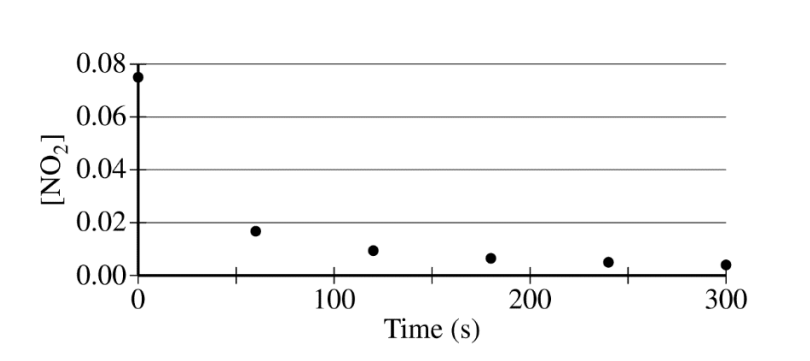
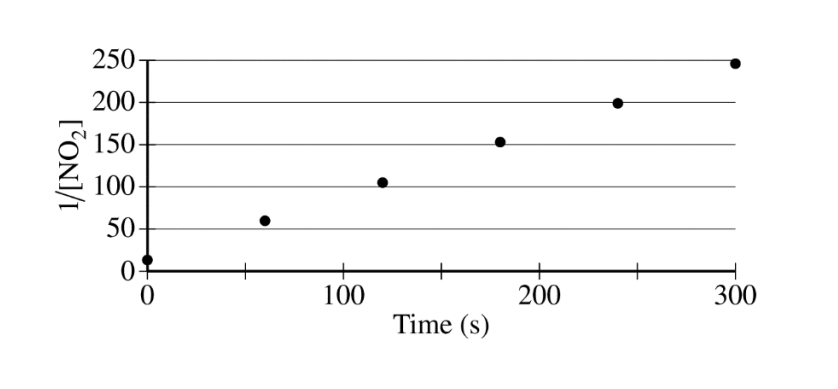
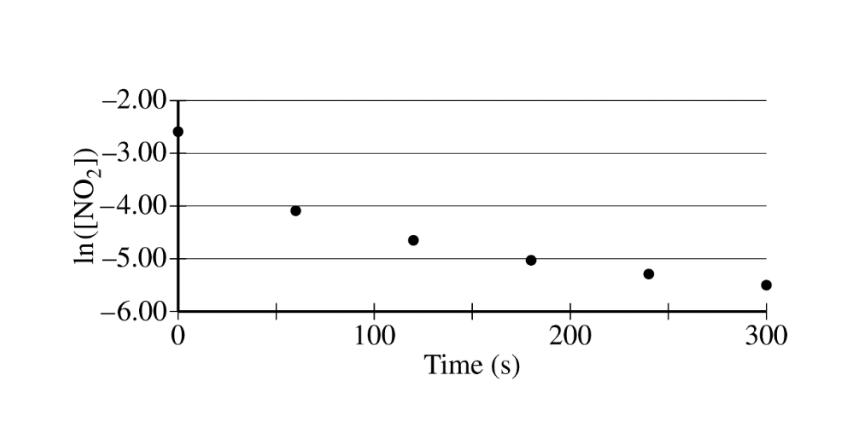
(a) Explain how the graphs indicate that the reaction is second order.
(b) Write the rate law for the decomposition of \(NO_2\)(g).
(c) Consider two possible mechanisms for the decomposition reaction.
(i) Is the rate law described by mechanism I shown below consistent with the rate law you wrote in part (b) ? Justify your answer.
Mechanism I
Step 1: NO2(g) + NO2(g) → NO(g) + NO3(g) slow
Step 2: NO3(g) → NO(g) + O2(g) fast
(ii) Is the rate law described by mechanism II shown below consistent with the rate law you wrote in part (b) ? Justify your answer.
Mechanism II
Step 1: NO2(g) + NO2(g) ⇔ N2O4(g) fast equilibrium
Step 2: N2O4(g) → 2 NO(g) + O2(g) slow
▶️Answer/Explanation
Ans:
(a)
| The linear graph of \(\frac{1}{[NO_{2}]}\) vs. time indicates a second-order reaction. |
(b)
| rate = k[NO2]2 |
(c) (i)
| Yes, Step 1 is slow, therefore it is the rate-determining step of this mechanism. The rate law of this elementary reaction is rate = k[NO2][NO2] = k[NO2]2, which is consistent with the second – order rate law in part (b). |
(ii)
| Yes, Step 2 is slow; therefore, it is the rate – determining step of this mechanism. The rate law of this elementary reaction is rate = k[N2O2]. Because N2O4 is an intermediate, it cannot appear in the rate law of the overall reaction. Because \(K_{eq}\frac{[N_{2}O_{4}]}{[NO_{2}]^{2}}\) in step 1, [N2O4] = Keq[NO2]2. Then, substituting Keq[NO2]2 for [N2O4] in the rate law of step 2 gives rate = (k Keq) [NO2]2 , which is consistent with the rate law in part (b). |
