Question
A student is asked to determine what mass of butane, \(C_4H_10\)(g), needs to burn in order to raise the temperature of a 1650 g beaker of sand by 180.°C. The student is provided with the equipment shown below.
(a) Calculate the amount of heat energy needed to raise the temperature of the beaker of sand by 180.°C. Assume that all the heat energy from the burner is transf erred to the beaker of sand and that the specific heat capacity of the beaker and sand together is 0.810 J/(g⋅°C). The student runs the experiment and collects the data shown in the table below.

(b) Calculate the number of moles of butane that was used in the experiment. Report your answer to the appropriate number of significant figures. The combustion of butane is represented by the equation below.
\(C_{4}H_{10}(g)+\frac{13}{2}O_{2}(g)\rightarrow 5H_{2}O(g)+4CO_{2}(g) \) \(\Delta ^{\circ}_{rxn}=-2659kj/mol_{rxn}\)
(c) Using the balanced equation for the combustion of butane and \(\Delta ^{\circ}_{rxn} \), determine the amount of heat energy produced by the combustion of butane in the experiment.
(d) The student claims that some of the heat energy produced by the combustion of butane was lost to the air surrounding the system. Do your answers to parts (a) and (c) support the student’s claim? Explain
▶️Answer/Explanation
.
(a)\( q= mc\Delta T\)
\(q=(1650g)\left ( 0.810\frac{j}{g.^{\circ}C} \right ) = 241,000 J = 241 kJ\)
(b) 225.26 g – 218.20 g = 7.06 g butane
\(7.06g\times \frac{1mol}{58.12g butane} = 0.121 mol butane\)
(c)\(0.121 mol butane \times \frac{2659kjproduced}{1mol butane}=322kj\)
(d) Yes, the answers to parts (a) and (c) support the hypothesis. The amount of heat generated from the combustion of the butane ism greater than the amount of heat required to cause the temperature change of the sand, indicating that some of the heat from the combustion of butane was lost.
Question
Answer the following questions relating to the chemistry of the halogens.
(a) The molecular formulas of diatomic bromine, chlorine, fluorine, and iodine are written below. Circle the formula of the molecule that has the longest bond length. Justify your choice in terms of atomic structure.
Br2 Cl2 F2 I2
A chemistry teacher wants to prepare Br2 . The teacher has access to the following three reagents: NaBr(aq), Cl2(g), and I2(s).
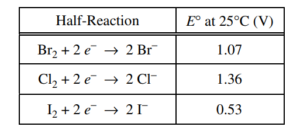
(b) Using the data in the table above, write the balanced equation for the thermodynamically favorable reaction that will produce Br2 when the teacher combines two of the reagents. Justify that the reaction is thermodynamically favorable by calculating the value of E° for the reaction.
Br2 and Cl2 can react to form the compound BrCl.
(c) The boiling point of Br2 is 332 K, whereas the boiling point of BrCl is 278 K. Explain this difference in boiling point in terms of all the intermolecular forces present between molecules of each substance.
The compound BrCl can decompose into Br2 and Cl2 , as represented by the balanced chemical equation below.
2 BrCl(g) ⇔ Br2(g) + Cl2(g) ΔH° = 1.6 kJ/molrxn
A 0.100 mole sample of pure BrCl(g) is placed in a previously evacuated, rigid 2.00 L container at 298 K. Eventually the system reaches equilibrium according to the equation above.
(d) Calculate the pressure in the container before equilibrium is established.
(e) Write the expression for the equilibrium constant, Keq , for the decomposition of BrCl.
After the system has reached equilibrium, 42 percent of the original BrCl sample has decomposed.
(f) Determine the value of Keq for the decomposition reaction of BrCl at 298 K.
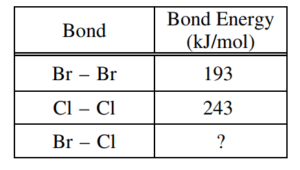
(g) Calculate the bond energy of the Br-Cl bond, in kJ/mol, using ΔH° for the reaction (1.6 kJ/molrxn) and the information in the following table.
▶️Answer/Explanation
Ans:
(a)
| I2 has the longest bond length because the radius of he I atom is greater than the radii of the other halogen atoms. Thus, the distance between the nuclei of atoms in I2 is greater than it is in smaller halogens. |
(b)
2 Br– + Cl → Br2 + 2 Cl– E0 = E0 (reduced species) – E0 (oxidized species) Because E0 for the reaction has a positive value, the reaction is thermodynamically favorable. |
(c)
| The only intermolecular attractions in Br2(l) are London forces, while those in BrCl(l) include both London forces and dipole-dipole forces. However, due to the greater polarizability of the electron cloud of Br2 compared to that of BrCl, the London forces in Br2(l) are stronger than the combined intermolecular forces in BrCl(l). Thus the boiling point of Br2(l) is greater than that of BrCl(l). |
(d)
| \(P=\frac{nRT}{V}=\frac{(0.100 mol)(0.08206 L atm mol^{-1}K^{-1})(298 K)}{2.00 L}=1.22 atm\) |
(e)
| \(K_{eq}=\frac{[Br_{2}][Cl_{2}]}{[BrCl]^{2}} \) or \(K_{eq}=\frac{P_{Br_{2}}P_{Cl_{2}}}{(P_{BrCl})^{2}}\) |
(f)
2 BrCl(g) ⇔ Br2(g) + Cl2(g)
PBrCl decomposed = (0.42) (1.22 atm) = 0.51 atm \(K_{eq}=\frac{(0.26)(0.26)}{(0.71)^{2}}=0.13\) Note: The solution is in terms of pressures. Solutions in terms of molar concentrations also earn full credit. |
(g)
ΔH0 = ∑ (bond energies) broken – ∑ (bond energies) formed 1.6 kJ/mol = 2(Br-Cl bond energy) – 193 kJ/mol + 243 kJ/mol) (436 + 1.6) kJ/mol = 2 (Br – Cl bond energy) Br – Cl bond energy = 219 kJ/mol |
